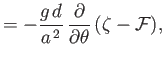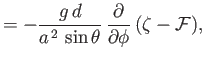

Next: Useful Lemma
Up: Terrestrial Ocean Tides
Previous: Global Ocean Tides
Non-Global Ocean Tides
Suppose that the surface of the Earth is covered by an ocean of uniform depth 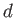 that extends from
that extends from 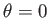 to
to
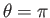 , and from
, and from
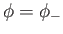 to
to
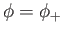 , where
, where
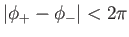 . For consistency with the previous analysis, we must imagine that
the remaining surface is covered by a frozen (i.e.,
. For consistency with the previous analysis, we must imagine that
the remaining surface is covered by a frozen (i.e., 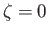 ) ocean of uniform depth
) ocean of uniform depth 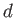 .
The motion of the ocean under the action of the tide generating potential is governed by
the Laplace tidal equations, (12.153)-(12.155), which are written
.
The motion of the ocean under the action of the tide generating potential is governed by
the Laplace tidal equations, (12.153)-(12.155), which are written
where
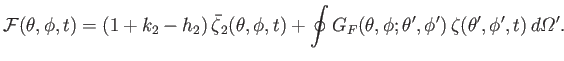 |
(12.184) |
The finite extent of the ocean in the 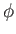 direction introduces the additional constraint
direction introduces the additional constraint
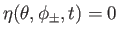 |
(12.185) |
into the problem.


Next: Useful Lemma
Up: Terrestrial Ocean Tides
Previous: Global Ocean Tides
Richard Fitzpatrick
2016-03-31
![$\displaystyle \frac{1}{\sin\theta}\left[\frac{\partial}{\partial\theta}\,(\sin\theta\,\xi)+ \frac{\partial\eta}{\partial\phi}\right] + \zeta$](img4654.png)