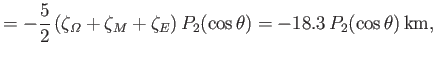Next: Global Ocean Tides
Up: Terrestrial Ocean Tides
Previous: Harmonics of Forcing Term
The 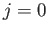 harmonic of the forcing term, which is associated with the Earth's axial rotation, is special, because the associated oscillation frequency is zero. In this
case, Equations (12.139)-(12.141) yield
harmonic of the forcing term, which is associated with the Earth's axial rotation, is special, because the associated oscillation frequency is zero. In this
case, Equations (12.139)-(12.141) yield  . Hence, it follows from Equations (12.129), (12.142) and
(12.143), as well as
Table 12.2, that
. Hence, it follows from Equations (12.129), (12.142) and
(12.143), as well as
Table 12.2, that
For the Earth-Moon-Sun system,
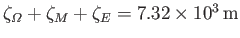 . Given the relatively large size of
. Given the relatively large size of
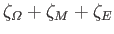 , we expect the
steady-state response to the equilibrium harmonic to be fluid-like (otherwise, the elastic stress within the Earth would exceed
the yield stress) (Fitzpatrick 2012). In other words,
, we expect the
steady-state response to the equilibrium harmonic to be fluid-like (otherwise, the elastic stress within the Earth would exceed
the yield stress) (Fitzpatrick 2012). In other words,
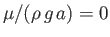 for the
for the 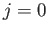 harmonic, which implies from Equations (12.97), (12.98), (12.101), and (12.102) that
harmonic, which implies from Equations (12.97), (12.98), (12.101), and (12.102) that 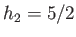 ,
, 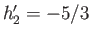 ,
, 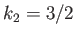 , and
, and  . Thus, it follows from the previous two equations that
. Thus, it follows from the previous two equations that
We deduce that the Earth's rotation causes a planetary equatorial (i.e.,
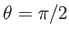 ) bulge of about
) bulge of about
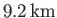 , and a polar (i.e.,
, and a polar (i.e., 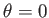 ) flattening of
) flattening of
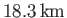 , but does not give rise to any
spatial variation in ocean depth. The observed equatorial bulge and polar flattening of the Earth are
, but does not give rise to any
spatial variation in ocean depth. The observed equatorial bulge and polar flattening of the Earth are
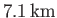 and
and
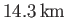 , respectively (Yoder 1995).
Our estimates for these values are too large because, for the sake of simplicity, we are treating the Earth as a uniform body. In reality, the Earth possesses a mass distribution
that is strongly concentrated in its core.
, respectively (Yoder 1995).
Our estimates for these values are too large because, for the sake of simplicity, we are treating the Earth as a uniform body. In reality, the Earth possesses a mass distribution
that is strongly concentrated in its core.



Next: Global Ocean Tides
Up: Terrestrial Ocean Tides
Previous: Harmonics of Forcing Term
Richard Fitzpatrick
2016-03-31
\,P_2(\cos\theta),$](img4639.png)
\,P_2(\cos\theta).$](img4641.png)
\,P_2(\cos\theta),$](img4639.png)
\,P_2(\cos\theta).$](img4641.png)