


Next: Harmonics of Forcing Term
Up: Terrestrial Ocean Tides
Previous: Planetary Response
In the co-rotating frame, the linearized (in 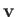 ) equations of motion of the ocean that covers the surface of the planet are (Fitzpatrick 2012)
) equations of motion of the ocean that covers the surface of the planet are (Fitzpatrick 2012)
where
 is the fluid velocity, and
is the fluid velocity, and
 the fluid pressure. Here,
the fluid pressure. Here,
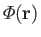 is the total gravitational
potential,
is the total gravitational
potential,
 the centrifugal potential (due to planetary rotation), and
the centrifugal potential (due to planetary rotation), and
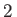
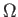
 the
Coriolis acceleration (likewise, due to planetary rotation). Furthermore, we have neglected the finite compressibility of
the fluid that makes up the ocean. Let
the
Coriolis acceleration (likewise, due to planetary rotation). Furthermore, we have neglected the finite compressibility of
the fluid that makes up the ocean. Let  ,
,  ,
, 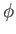 be spherical
coordinates in the co-rotating frame, and let
be spherical
coordinates in the co-rotating frame, and let 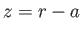 . It is helpful to define
. It is helpful to define
 ,
, 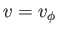 , and
, and 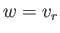 . Assuming that
. Assuming that
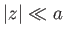 , the previous equations of motion reduce to
, the previous equations of motion reduce to
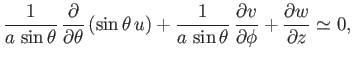 |
(12.102) |
and
In accordance with Equations (12.45), (12.47), and (12.53), the lower and upper surfaces of the ocean lie at
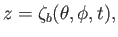 |
(12.106) |
and
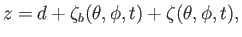 |
(12.107) |
respectively, where
 |
(12.108) |
It follows that
Let us assume that
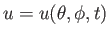 and
and
 : that is, the horizontal components of the fluid velocity are independent of
: that is, the horizontal components of the fluid velocity are independent of  . Integration of
Equation (12.105) from
. Integration of
Equation (12.105) from  to
to 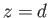 , making use of the previous two boundary conditions, yields
, making use of the previous two boundary conditions, yields
![$\displaystyle \frac{\partial \zeta}{\partial t}= - \frac{d}{a\,\sin\theta}\left...
...rtial}{\partial\theta}\,(\sin\theta\,u)+\frac{\partial v}{\partial\phi}\right].$](img4477.png) |
(12.111) |
Equations (12.112)-(12.114) imply that
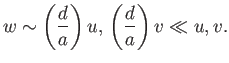 |
(12.112) |
In accordance with the analysis of Section 12.8, we can write
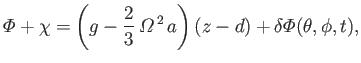 |
(12.113) |
where
 is the total perturbing potential due to tidal, rotation, and ocean self-gravity, effects. We
have neglected an unimportant constant term. We have also neglected the
is the total perturbing potential due to tidal, rotation, and ocean self-gravity, effects. We
have neglected an unimportant constant term. We have also neglected the  -dependence of the perturbing potential, because the variation lengthscale of this
potential is
-dependence of the perturbing potential, because the variation lengthscale of this
potential is  , rather than
, rather than  , so that
, so that
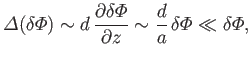 |
(12.114) |
where
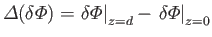 .
Let us assume that the ocean is in approximate vertical force balance: that is,
.
Let us assume that the ocean is in approximate vertical force balance: that is,
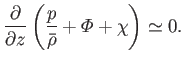 |
(12.115) |
It follows that
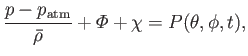 |
(12.116) |
where
 is the (uniform and constant) pressure of the atmosphere.
However, pressure balance at the ocean's upper surface requires that
is the (uniform and constant) pressure of the atmosphere.
However, pressure balance at the ocean's upper surface requires that
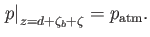 |
(12.117) |
Hence, we deduce that
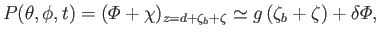 |
(12.118) |
to first order in small quantities [i.e., 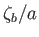 ,
, 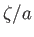 ,
,
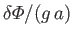 , and
, and
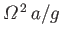 ]. Thus, Equations (12.106), (12.107),
and (12.115) yield
]. Thus, Equations (12.106), (12.107),
and (12.115) yield
Let us justify our previous assumption that the ocean is in approximate vertical force balance. Equations (12.108), (12.115), and (12.119)
imply that
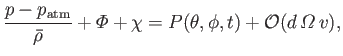 |
(12.121) |
where we have assumed that
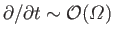 and
and
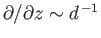 . However, Equations (12.121)-(12.123) yield
. However, Equations (12.121)-(12.123) yield
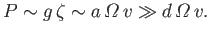 |
(12.122) |
Hence, Equation (12.124) becomes
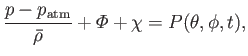 |
(12.123) |
which is equivalent to Equation (12.119).
Let us justify our previous assumption that 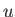 only depends weakly on
only depends weakly on  . It follows from Equations (12.117) and
(12.122)
that
. It follows from Equations (12.117) and
(12.122)
that
where
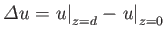 . In a similar manner, it can be shown that
. In a similar manner, it can be shown that
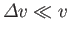 .
.
According to Equations (12.95) and (12.100),
Hence, Equations (12.114), (12.122), and (12.123) give
We can write
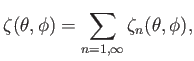 |
(12.131) |
where [cf., Equation (12.37)]
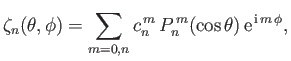 |
(12.132) |
and the 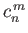 are arbitrary complex constants.
Now, (Abramowitz and Stegun 1965)
are arbitrary complex constants.
Now, (Abramowitz and Stegun 1965)
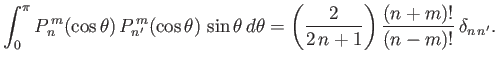 |
(12.133) |
Hence,
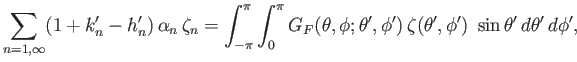 |
(12.134) |
where
is termed the Farrell Green's function (Farrell 1972).
It follows that
where
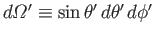 .
Equations (12.139)-(12.141) are known collectively as the Laplace tidal equations, because they were first derived (in simplified form) by Laplace (Lamb 1993).
.
Equations (12.139)-(12.141) are known collectively as the Laplace tidal equations, because they were first derived (in simplified form) by Laplace (Lamb 1993).
The Laplace tidal equations are a closed set of equations for the perturbed ocean depth,
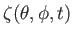 , and the polar and
azimuthal components of the horizontal ocean velocity,
, and the polar and
azimuthal components of the horizontal ocean velocity,
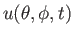 , and
, and
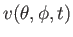 , respectively. Here,
, respectively. Here,  is the planetary radius,
is the planetary radius, 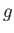 the
mean gravitational acceleration at the planetary surface,
the
mean gravitational acceleration at the planetary surface,  the mean ocean depth,
the mean ocean depth,
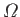 the planetary angular rotation velocity, and
the planetary angular rotation velocity, and 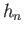 ,
, 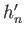 ,
, 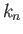 ,
, 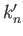 are Love numbers defined in Equations (12.97), (12.98), (12.101), and (12.102), respectively. Amongst other things, the Love numbers
determine the elastic response of the planet to the forcing term,
are Love numbers defined in Equations (12.97), (12.98), (12.101), and (12.102), respectively. Amongst other things, the Love numbers
determine the elastic response of the planet to the forcing term,
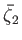 .
Finally, the Farrell Green's function parameterizes the self-gravity of the ocean.
.
Finally, the Farrell Green's function parameterizes the self-gravity of the ocean.
Table 12.1:
The principal harmonics of the forcing term in the Laplace tidal equations.

|
|
|
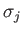
|
Classification |
| |
|
|
|
|
| |
|
|
|
|
| 0
|
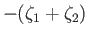
|
0
|
0
|
Equilibrium |
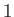
|
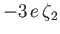
|
0
|
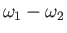
|
Long Period |
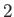
|
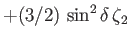
|
0
|
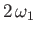
|
Long Period |

|
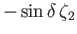
|
|

|
Diurnal |
|
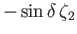
|
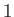
|
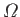
|
Diurnal |
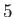
|
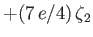
|
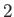
|
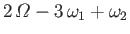
|
Semi-diurnal |

|
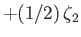
|
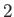
|

|
Semi-diurnal |
|



Next: Harmonics of Forcing Term
Up: Terrestrial Ocean Tides
Previous: Planetary Response
Richard Fitzpatrick
2016-03-31

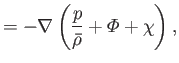

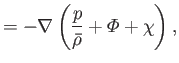
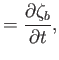
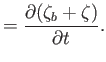
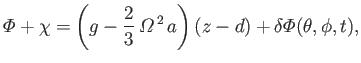
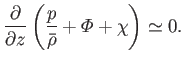
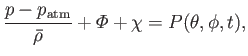
![]() only depends weakly on
only depends weakly on ![]() . It follows from Equations (12.117) and
(12.122)
that
. It follows from Equations (12.117) and
(12.122)
that

![$\displaystyle = \sum_{n=1,\infty}\left[h_2\,\skew{5}\bar{\zeta}_2\,\delta_{n\,2} + h_n'\,\alpha_n\,\zeta_n\right],$](img4504.png)
![$\displaystyle = \sum_{n=1,\infty}\left[(1+k_2)\,\skew{5}\bar{\zeta}_2\,\delta_{n\,2} + (1+k_n')\,\alpha_n\,\zeta_n\right].$](img4506.png)
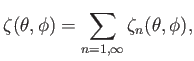
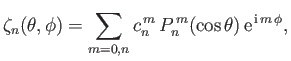
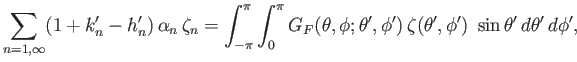
![]() , and the polar and
azimuthal components of the horizontal ocean velocity,
, and the polar and
azimuthal components of the horizontal ocean velocity,
![]() , and
, and
![]() , respectively. Here,
, respectively. Here, ![]() is the planetary radius,
is the planetary radius, ![]() the
mean gravitational acceleration at the planetary surface,
the
mean gravitational acceleration at the planetary surface, ![]() the mean ocean depth,
the mean ocean depth,
![]() the planetary angular rotation velocity, and
the planetary angular rotation velocity, and ![]() ,
, ![]() ,
, ![]() ,
, ![]() are Love numbers defined in Equations (12.97), (12.98), (12.101), and (12.102), respectively. Amongst other things, the Love numbers
determine the elastic response of the planet to the forcing term,
are Love numbers defined in Equations (12.97), (12.98), (12.101), and (12.102), respectively. Amongst other things, the Love numbers
determine the elastic response of the planet to the forcing term,
![]() .
Finally, the Farrell Green's function parameterizes the self-gravity of the ocean.
.
Finally, the Farrell Green's function parameterizes the self-gravity of the ocean.