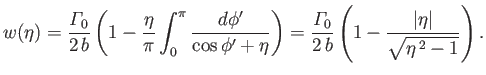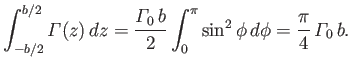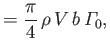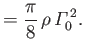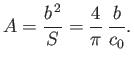Next: Simple Flight Problems
Up: Incompressible Aerodynamics
Previous: Aerodynamic Forces
Ellipsoidal Airfoils
Consider an ellipsoidal airfoil whose outer surface is specified by the parametric equations
where
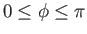 and
and
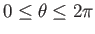 . Here,
. Here, 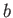 is the wingspan,
is the wingspan, 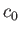 the maximum wing width, and
the maximum wing width, and  the
maximum wing thickness. Note that the wing's cross-section is elliptical both in the
the
maximum wing thickness. Note that the wing's cross-section is elliptical both in the  -
- and the
and the  -
- planes. It is
assumed that
planes. It is
assumed that
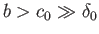 : that is, the wingspan is greater than the wing width, which in turn is much
greater than the wing thickness. At fixed
: that is, the wingspan is greater than the wing width, which in turn is much
greater than the wing thickness. At fixed 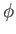 (i.e., fixed
(i.e., fixed  ), the width and thickness of the airfoil are
), the width and thickness of the airfoil are
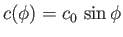 and
and
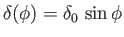 ,
respectively.
,
respectively.
Assuming that the two-dimensional result (9.44) holds at fixed  , we deduce that the air circulation about the wing
satisfies
, we deduce that the air circulation about the wing
satisfies
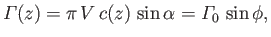 |
(9.94) |
where
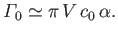 |
(9.95) |
Here, the angle of attack,  , is assumed to be small.
From Equations (9.90) and (9.94), the downwash velocity in the region
, is assumed to be small.
From Equations (9.90) and (9.94), the downwash velocity in the region 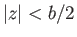 is given by
is given by
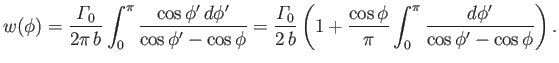 |
(9.96) |
The integrand appearing in the integral
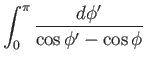 |
(9.97) |
is singular when
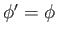 . However, we can still obtain a finite value for the integral by taking its Cauchy principal part: that is,
. However, we can still obtain a finite value for the integral by taking its Cauchy principal part: that is,
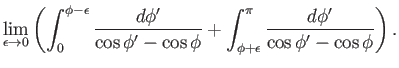 |
(9.98) |
Physically, this is equivalent to omitting the contribution of the local free vortex at a given point on the airfoil's trailing edge to the downwash
velocity induced at that point, which is reasonable because a vortex induces zero velocity at its center.
Hence, we obtain
which implies that
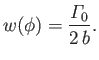 |
(9.100) |
In the region 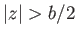 , we can write
, we can write
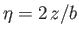 , so that
, so that
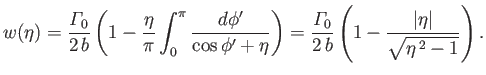 |
(9.101) |
Hence, we conclude that the downwash velocity profile induced by an ellipsoidal airfoil takes the form
 |
(9.102) |
This profile is shown in Figure 9.13. It can be seen that the downwash velocity is uniform and positive in the region between the wingtips (i.e.,
 ), but negative and decaying in the region outside the wingtips. Hence, we conclude that as air passes over an airfoil subject to
an upward lift it acquires a net downward velocity component, which, of course, is a consequence of the reaction to the
lift. On the other hand, the air immediately behind and to the sides of the airfoil acquires a net upward velocity component. In other
words, the lift acting on the airfoil is associated with a downwash of air directly behind, and an upwash behind and to either side of,
the airfoil. The existence of upwash slightly behind and to the side of a flying object allows us to explain the V-formation adopted
by wild geese--a bird flying in the upwash of another bird needs to generate less lift in order to stay in the air, and, consequently, experiences
less induced drag.
), but negative and decaying in the region outside the wingtips. Hence, we conclude that as air passes over an airfoil subject to
an upward lift it acquires a net downward velocity component, which, of course, is a consequence of the reaction to the
lift. On the other hand, the air immediately behind and to the sides of the airfoil acquires a net upward velocity component. In other
words, the lift acting on the airfoil is associated with a downwash of air directly behind, and an upwash behind and to either side of,
the airfoil. The existence of upwash slightly behind and to the side of a flying object allows us to explain the V-formation adopted
by wild geese--a bird flying in the upwash of another bird needs to generate less lift in order to stay in the air, and, consequently, experiences
less induced drag.
Figure 9.13:
Downwash velocity profile induced at the trailing edge by an ellipsoidal airfoil.
 |
It follows from Equation (9.93) and (9.94) that
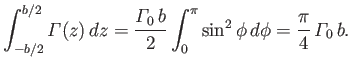 |
(9.103) |
Hence, Equation (9.80), (9.82), and (9.100) yield the following expression for the lift and induced drag acting on an ellipsoidal
airfoil,
The surface area of the airfoil in the  -
- plane is
plane is
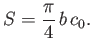 |
(9.106) |
Moreover, the airfoil's aspect-ratio is conventionally defined as the length to width ratio for a rectangle of length 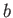 that has the same
area as the airfoil: that is,
that has the same
area as the airfoil: that is,
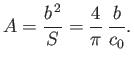 |
(9.107) |
It thus follows from Equation (9.95) that
where
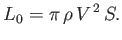 |
(9.110) |



Next: Simple Flight Problems
Up: Incompressible Aerodynamics
Previous: Aerodynamic Forces
Richard Fitzpatrick
2016-03-31
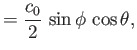
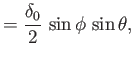
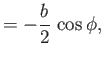
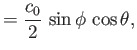
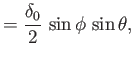
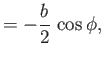
![]() , we deduce that the air circulation about the wing
satisfies
, we deduce that the air circulation about the wing
satisfies
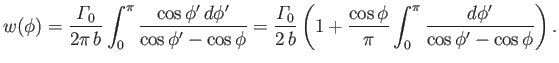
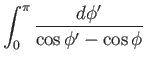
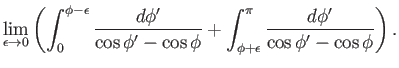
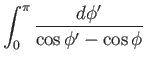
![$\displaystyle =\lim_{\epsilon\rightarrow 0}\left\{\left(\frac{1}{\sin\phi}\,\ln...
...\phi+\phi')} {\sin\,(1/2)\,(\phi-\phi')}\right]\right)_0^{\phi-\epsilon}\right.$](img3497.png)
![$\displaystyle \phantom{=}\left.+\left(\frac{1}{\sin\phi}\,\ln\left[\frac{\sin\,...
...i'+\phi)} {\sin\,(1/2)\,(\phi'-\phi)}\right]\right)_\pi^{\phi+\epsilon}\right\}$](img3498.png)
![$\displaystyle =\lim_{\epsilon\rightarrow 0}\left(\frac{1}{\sin\phi}\,\ln\left[\frac{\sin(\phi-\epsilon/2)}{\sin(\phi+\epsilon/2)}\right]\right) = 0,$](img3499.png)