![$\displaystyle \frac{u(x,y)}{U(x)} = F\left[\left(\frac{U_0}{\nu}\right)^{1/2}\,\frac{y}{x}\right],
$](img3235.png)
where
subject to the boundary conditions
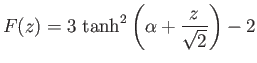
is a suitable solution of the previous differential equation, where
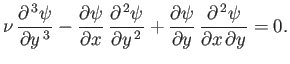
Here, the symmetry axis of the jet is assumed to run along the
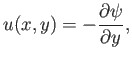
where
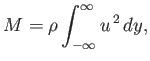
to be independent of
Consider a self-similar stream function of the form
Demonstrate that the boundary layer equation requires that
Suppose that
Demonstrate that
subject to the constraints that
is a suitable solution, and that
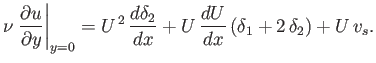
Suppose that
![$\displaystyle u(x,y) = U(x)\left\{\begin{array}{lcl}
\sin(\alpha\,y)&\mbox{\hsp...
...0\leq y\leq \pi/(2\,\alpha)\\ [0.5ex]
1&&y>\pi/(2\,\alpha)
\end{array}\right.,
$](img3262.png)
where
respectively. Hence, deduce that
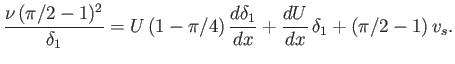
Consider a boundary layer on a flat plate, for which ![]() . Show that, in the absence of suction,
. Show that, in the absence of suction,
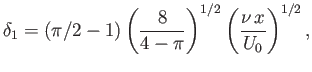
but that in the presence of suction
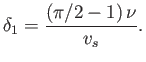
Hence, deduce that, for a plate of length
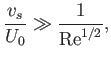
where