


Next: Flow Past a Cylindrical
Up: Two-Dimensional Incompressible Inviscid Flow
Previous: Two-Dimensional Vortex Filaments
In a two-dimensional flow pattern, we can automatically satisfy the
incompressibility constraint,
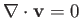 , by expressing the pattern in terms of a stream function. Suppose, however, that, in addition
to being incompressible, the flow pattern is also irrotational. In this case,
Equation (5.10) yields
, by expressing the pattern in terms of a stream function. Suppose, however, that, in addition
to being incompressible, the flow pattern is also irrotational. In this case,
Equation (5.10) yields
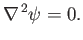 |
(5.60) |
In cylindrical coordinates, because
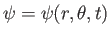 , this expression implies that (see Section C.3)
, this expression implies that (see Section C.3)
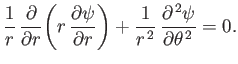 |
(5.61) |
Let us search for a separable solution of Equation (5.61) of the form
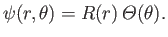 |
(5.62) |
It is easily seen that
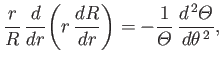 |
(5.63) |
which can only be satisfied if
where 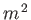 is an arbitrary (positive) constant. The general solution of Equation (5.65)
is a linear combination of
is an arbitrary (positive) constant. The general solution of Equation (5.65)
is a linear combination of
 and
and
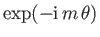 factors.
However, assuming that the flow extends over all
factors.
However, assuming that the flow extends over all 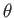 values, the function
values, the function
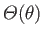 must be single-valued in
must be single-valued in 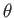 , otherwise
, otherwise
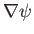 --and,
hence,
--and,
hence, 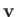 --would not be be single-valued (which is unphysical). It follows that
--would not be be single-valued (which is unphysical). It follows that 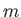 can only take integer values (and that
can only take integer values (and that 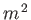 must be a positive, rather than a negative, constant).
The general solution of Equation (5.64) is a linear combination of
must be a positive, rather than a negative, constant).
The general solution of Equation (5.64) is a linear combination of 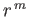 and
and
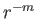 factors, except for the special case
factors, except for the special case 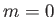 , when it is a linear combination
of
, when it is a linear combination
of 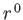 and
and 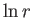 factors. Thus, the general stream function for steady two-dimensional
irrotational flow (that extends over all values of
factors. Thus, the general stream function for steady two-dimensional
irrotational flow (that extends over all values of 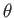 ) takes the form
) takes the form
![$\displaystyle \psi(r,\theta) = \alpha_0+ \beta_0\,\ln r + \sum_{m>0} (\alpha_m\,r^{\,m}+\beta_m\,r^{-m})\, \sin[m\,(\theta-\theta_m)],$](img1746.png) |
(5.66) |
where 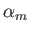 ,
, 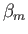 , and
, and 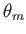 are arbitrary constants.
We can recognize the first few terms on the right-hand side of the previous expression. The constant term
are arbitrary constants.
We can recognize the first few terms on the right-hand side of the previous expression. The constant term 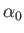 has zero gradient, and, therefore, does not give rise to any flow. The term
has zero gradient, and, therefore, does not give rise to any flow. The term
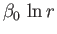 is the flow pattern generated by
a vortex filament of intensity
is the flow pattern generated by
a vortex filament of intensity
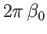 , coincident with the
, coincident with the 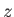 -axis. (See Section 5.6.) The
term
-axis. (See Section 5.6.) The
term
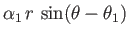 corresponds to uniform flow of speed
corresponds to uniform flow of speed 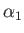 whose
direction subtends a (counter-clockwise) angle
whose
direction subtends a (counter-clockwise) angle 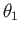 with the minus
with the minus  -axis. (See Section 5.4.)
Finally, the term
-axis. (See Section 5.4.)
Finally, the term
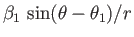 corresponds to a dipole flow pattern. (See Section 5.5.)
corresponds to a dipole flow pattern. (See Section 5.5.)
The velocity potential associated with the irrotational stream function (5.66) satisfies [see Equations (4.89) and
(5.7)]
It follows that
![$\displaystyle \phi(r,\theta) = \alpha_0-\beta_0\,\theta+\sum_{m>0}(\alpha_m\,r^{\,m}-\beta_m\,r^{-m})\,\cos[m\,(\theta-\theta_0)].$](img1759.png) |
(5.69) |
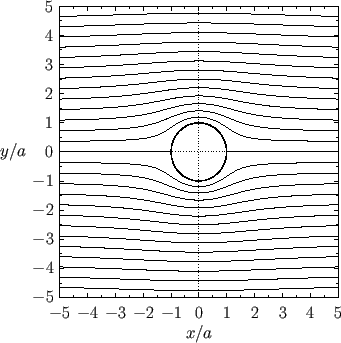
Figure:
Streamlines of the flow generated by a cylindrical obstacle of radius 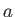 , whose axis runs along the
, whose axis runs along the 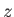 -axis,
placed in the uniform flow field
-axis,
placed in the uniform flow field
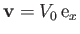 . The normalized circulation is
. The normalized circulation is 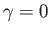 .
.
 |



Next: Flow Past a Cylindrical
Up: Two-Dimensional Incompressible Inviscid Flow
Previous: Two-Dimensional Vortex Filaments
Richard Fitzpatrick
2016-01-22
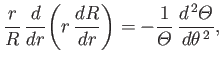
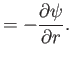
![$\displaystyle \phi(r,\theta) = \alpha_0-\beta_0\,\theta+\sum_{m>0}(\alpha_m\,r^{\,m}-\beta_m\,r^{-m})\,\cos[m\,(\theta-\theta_0)].$](img1759.png)
