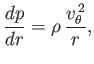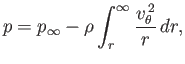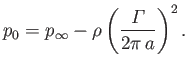Next: Two-Dimensional Irrotational Flow in
Up: Two-Dimensional Incompressible Inviscid Flow
Previous: Two-Dimensional Sources and Sinks
Two-Dimensional Vortex Filaments
Consider a vortex filament of intensity
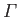 that is coincident with the
that is coincident with the  -axis. By symmetry, we expect the associated flow pattern to circulate isotropically around the filament.
(See Figure 5.5.) In other words, we expect
-axis. By symmetry, we expect the associated flow pattern to circulate isotropically around the filament.
(See Figure 5.5.) In other words, we expect
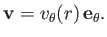 |
(5.45) |
According to Section 4.13,
the circulation,
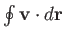 , around any closed curve in the
, around any closed curve in the  -
- plane is equal to the net intensity of the vortex filaments that pass through the curve. Consider a circular curve of radius
plane is equal to the net intensity of the vortex filaments that pass through the curve. Consider a circular curve of radius 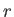 that is concentric with the origin. It follows that
that is concentric with the origin. It follows that
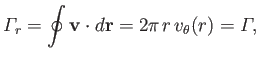 |
(5.46) |
or
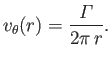 |
(5.47) |
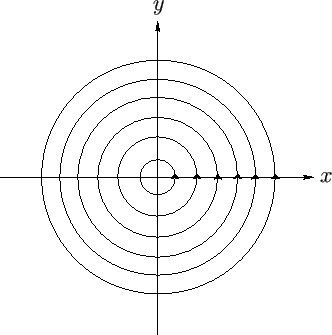
Figure:
Streamlines of the flow generated by a line vortex coincident with the  -axis.
-axis.
 |
According to Equations (5.13) and (5.14), the stream function associated with a vortex filament
of intensity
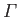 that is coincident with the
that is coincident with the  -axis is
-axis is
 |
(5.48) |
Note that the streamlines,  , circulate around the
, circulate around the  -axis, as illustrated in Figure 5.5.
-axis, as illustrated in Figure 5.5.
It can be seen, from Equation (5.48), that
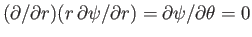 .
Hence,
it follows from Equation (5.15) that
.
Hence,
it follows from Equation (5.15) that
 . In other words, the flow pattern
associated with a straight vortex filament is irrotational. This is a somewhat surprising result, because there
is a net circulation of the flow around the filament, and, according to Section 4.13, non-zero circulation implies
non-zero vorticity. The paradox can be resolved by supposing that the filament has a small,
but finite, radius. In fact, let the filament have the finite radius
. In other words, the flow pattern
associated with a straight vortex filament is irrotational. This is a somewhat surprising result, because there
is a net circulation of the flow around the filament, and, according to Section 4.13, non-zero circulation implies
non-zero vorticity. The paradox can be resolved by supposing that the filament has a small,
but finite, radius. In fact, let the filament have the finite radius 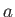 , and be such that the vorticity is
uniform inside this radius, and zero outside: that is,
, and be such that the vorticity is
uniform inside this radius, and zero outside: that is,
![$\displaystyle \omega_z = \left\{\begin{array}{lll} {\mit\Gamma}/(\pi\,a^{\,2})&\mbox{\hspace{1cm}}&r\leq a\\ [0.5ex] 0&&r>a \end{array}\right..$](img1710.png) |
(5.49) |
Note that the intensity of the filament (i.e., the product of its vorticity and cross-sectional
area) is still
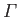 . According to Equation (5.15), and assuming that
. According to Equation (5.15), and assuming that
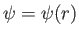 ,
,
![$\displaystyle \frac{1}{r}\,\frac{d}{\partial r}\!\left(r\,\frac{d\psi}{d r}\rig...
...(\pi\,a^{\,2})&\mbox{\hspace{1cm}}&r\leq a\\ [0.5ex] 0&&r>a \end{array}\right..$](img1712.png) |
(5.50) |
The solution that is well behaved at  , and continuous (up to its first derivative) at
, and continuous (up to its first derivative) at  , is
, is
![$\displaystyle \psi(r,\theta)= \left\{\begin{array}{lll} ({\mit\Gamma}/4\pi)\,(r...
...{1cm}}&r\leq a\\ [0.5ex] ({\mit\Gamma}/2\pi)\,\ln(r/a)&&r>a \end{array}\right..$](img1715.png) |
(5.51) |
This expression is equivalent to Equation (5.48) (apart from an unimportant additive constant) outside the filament, but
differs inside. The associated circulation velocity,
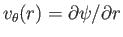 , is
, is
![$\displaystyle v_\theta(r)= \left\{\begin{array}{lll} ({\mit\Gamma}/2\pi)\,(r/a^...
...ace{1cm}}&r\leq a\\ [0.5ex] ({\mit\Gamma}/2\pi)\,(1/r)&&r>a \end{array}\right.,$](img1717.png) |
(5.52) |
whereas the circulation,
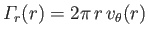 , is written
, is written
![$\displaystyle {\mit\Gamma}_r(r)= \left\{\begin{array}{lll} {\mit\Gamma}\,(r/a)^2&\mbox{\hspace{1cm}}&r\leq a\\ [0.5ex] {\mit\Gamma}&&r>a \end{array}\right..$](img1719.png) |
(5.53) |
Thus, we conclude that the flow pattern associated with a straight vortex filament is irrotational
outside the filament, but has finite vorticity inside the filament. Moreover, the non-zero internal
vorticity generates a constant net circulation of the flow outside the filament. In the limit in which the
radius of the filament tends to zero, the vorticity within the filament tends to infinity
(in such a way that the product of the vorticity and the cross-sectional area of the filament remains
constant), and the region of the fluid in which the vorticity is non-zero becomes infinitesimal in extent.
Let us determined the pressure profile in the vicinity of a vortex filament of finite radius. Assuming, from symmetry, that 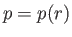 , Equation (1.149),
yields
, Equation (1.149),
yields
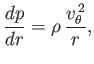 |
(5.54) |
which can be integrated to give
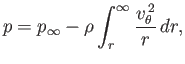 |
(5.55) |
where 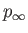 is the pressure at infinity. Making use of expression (5.52), we obtain
is the pressure at infinity. Making use of expression (5.52), we obtain
 |
(5.56) |
It follows that the minimum pressure occurs at the center of the vortex ( ), and takes the value
), and takes the value
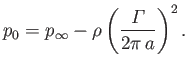 |
(5.57) |
Under normal circumstances, the pressure in a fluid must remain positive, which implies that a vortex
filament of intensity
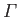 , embedded in a fluid of density
, embedded in a fluid of density  and background pressure
and background pressure
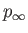 , has a minimum radius of order
, has a minimum radius of order
 |
(5.58) |
Finally, because the flow pattern outside a straight vortex filament is irrotational, it can be derived from a velocity potential.
It is easily demonstrated that the appropriate potential takes the form
 |
(5.59) |
Note that the previous potential is multivalued. However, this does not cause any
particular difficulty,
because the potential is continuous, and its gradient is single valued.



Next: Two-Dimensional Irrotational Flow in
Up: Two-Dimensional Incompressible Inviscid Flow
Previous: Two-Dimensional Sources and Sinks
Richard Fitzpatrick
2016-01-22
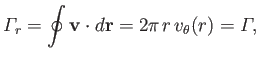
![]() that is coincident with the
that is coincident with the ![]() -axis is
-axis is
![]() .
Hence,
it follows from Equation (5.15) that
.
Hence,
it follows from Equation (5.15) that
![]() . In other words, the flow pattern
associated with a straight vortex filament is irrotational. This is a somewhat surprising result, because there
is a net circulation of the flow around the filament, and, according to Section 4.13, non-zero circulation implies
non-zero vorticity. The paradox can be resolved by supposing that the filament has a small,
but finite, radius. In fact, let the filament have the finite radius
. In other words, the flow pattern
associated with a straight vortex filament is irrotational. This is a somewhat surprising result, because there
is a net circulation of the flow around the filament, and, according to Section 4.13, non-zero circulation implies
non-zero vorticity. The paradox can be resolved by supposing that the filament has a small,
but finite, radius. In fact, let the filament have the finite radius ![]() , and be such that the vorticity is
uniform inside this radius, and zero outside: that is,
, and be such that the vorticity is
uniform inside this radius, and zero outside: that is,
![$\displaystyle \omega_z = \left\{\begin{array}{lll} {\mit\Gamma}/(\pi\,a^{\,2})&\mbox{\hspace{1cm}}&r\leq a\\ [0.5ex] 0&&r>a \end{array}\right..$](img1710.png)
![$\displaystyle \frac{1}{r}\,\frac{d}{\partial r}\!\left(r\,\frac{d\psi}{d r}\rig...
...(\pi\,a^{\,2})&\mbox{\hspace{1cm}}&r\leq a\\ [0.5ex] 0&&r>a \end{array}\right..$](img1712.png)
![$\displaystyle \psi(r,\theta)= \left\{\begin{array}{lll} ({\mit\Gamma}/4\pi)\,(r...
...{1cm}}&r\leq a\\ [0.5ex] ({\mit\Gamma}/2\pi)\,\ln(r/a)&&r>a \end{array}\right..$](img1715.png)
![$\displaystyle {\mit\Gamma}_r(r)= \left\{\begin{array}{lll} {\mit\Gamma}\,(r/a)^2&\mbox{\hspace{1cm}}&r\leq a\\ [0.5ex] {\mit\Gamma}&&r>a \end{array}\right..$](img1719.png)
![]() , Equation (1.149),
yields
, Equation (1.149),
yields