


Next: Energy of a Floating
Up: Hydrostatics
Previous: Angular Stability of Floating
Suppose that the floating body considered in the previous section is in an equilibrium state.
Let 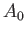 be the cross-sectional area at the waterline: that is, in the plane
be the cross-sectional area at the waterline: that is, in the plane  . Because the
body is assumed to be symmetric with respect to
the
. Because the
body is assumed to be symmetric with respect to
the  and
and 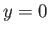 planes, we have
planes, we have
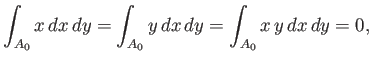 |
(2.22) |
where the integrals are taken over the whole cross-section at  .
Let
.
Let
 be the body's draft: that is, the vertical distance between the surface of the water and the body's lower boundary. It follows, from symmetry, that
be the body's draft: that is, the vertical distance between the surface of the water and the body's lower boundary. It follows, from symmetry, that
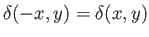 and
and
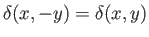 . Moreover, the submerged volume is
. Moreover, the submerged volume is
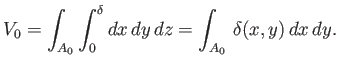 |
(2.23) |
It also follows from symmetry that
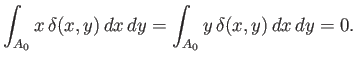 |
(2.24) |
The depth of the unperturbed center of buoyancy below the surface of the water is
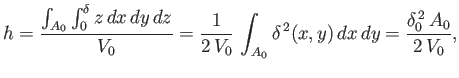 |
(2.25) |
where
![$\displaystyle \delta_0 = \left[\frac{\int_{A_0}\delta^{\,2}(x,y)\,dx\,dy}{A_0}\right]^{1/2}.$](img634.png) |
(2.26) |
Finally, from symmetry, the unperturbed center of buoyancy lies at 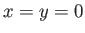 .
.
Suppose that the body now turns through a small angle 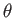 about the
about the  -axis.
As is easily demonstrated, the body's new draft becomes
-axis.
As is easily demonstrated, the body's new draft becomes
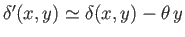 . Hence, the new submerged volume is
. Hence, the new submerged volume is
![$\displaystyle V_0'=\int_{A_0} [\delta(x,y) -\theta\,y]\,dx\,dy = V_0 + \theta\int_{A_0} y\,dx\,dy = V_0,$](img637.png) |
(2.27) |
where use has been made of Equations (2.22) and (2.23). Thus, the submerged volume is
unchanged, as should be the case for a purely angular displacement. The new depth of the center of buoyancy is
![$\displaystyle h' = \frac{\int_{A_0}\int_0^{\delta'} z\,dx\,dy\,dz}{V_0}=\frac{1...
...\,2}(x,y) -2\,\theta\,y\,\delta(x,y) + {\cal O}(\theta^{\,2})\right]dx\,dy = h,$](img638.png) |
(2.28) |
where use has been made of Equations (2.24) and (2.25). Thus, the depth of the center of buoyancy is also unchanged. Moreover, from symmetry, it
is clear that the center of buoyancy still lies at  . Finally, the new
. Finally, the new  -coordinate of
the center of buoyancy is
-coordinate of
the center of buoyancy is
![$\displaystyle \frac{\int_{A_0}\int_0^{\delta'}y\,dx\,dy\,dz}{V_0}=\frac{\int_{A...
...[\delta(x,y)-\theta\,y]\,dx\,dy}{V_0}=-\theta\,\frac{\kappa_x^{\,2}\,A_0}{V_0},$](img639.png) |
(2.29) |
where use has been made of Equation (2.24). Here,
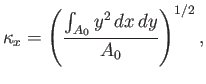 |
(2.30) |
is the radius of gyration of area 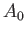 about the
about the  -axis.
-axis.
It follows, from the previous analysis, that if the floating body under consideration turns through a
small angle 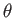 about the
about the  -axis then its center of buoyancy shifts horizontally a distance
-axis then its center of buoyancy shifts horizontally a distance
 in the plane perpendicular to the axis of rotation.
In other words, the distance
in the plane perpendicular to the axis of rotation.
In other words, the distance 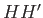 in Figure 2.1 is
in Figure 2.1 is
 . Simple trigonometry
reveals that
. Simple trigonometry
reveals that
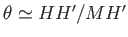 (assuming that
(assuming that 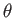 is small). Hence,
is small). Hence,
 . Now,
. Now, 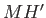 is the height of the metacenter
relative to the center of buoyancy. However, the center of buoyancy lies a depth
is the height of the metacenter
relative to the center of buoyancy. However, the center of buoyancy lies a depth  below the surface of the water (which corresponds to the plane
below the surface of the water (which corresponds to the plane  ).
Hence, the
).
Hence, the  -coordinate of the metacenter is
-coordinate of the metacenter is
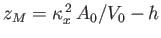 . Finally, if
. Finally, if 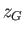 and
and 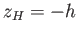 are the
are the  -coordinates of the unperturbed
centers of gravity and buoyancy, respectively, then
-coordinates of the unperturbed
centers of gravity and buoyancy, respectively, then
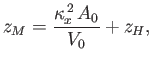 |
(2.31) |
and
the metacentric height,
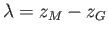 , becomes
, becomes
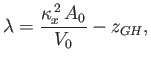 |
(2.32) |
where
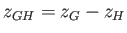 . Note that, because
. Note that, because
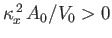 , the metacenter always lies above
the center of buoyancy.
, the metacenter always lies above
the center of buoyancy.
A simple extension of the previous argument reveals that if the body turns through
a small angle 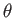 about the
about the  -axis then the metacentric height is
-axis then the metacentric height is
 |
(2.33) |
where
 |
(2.34) |
is radius of gyration of area 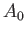 about the
about the  -axis. Finally, as is easily demonstrated, if the body rotates about a
horizontal axis which subtends an angle
-axis. Finally, as is easily demonstrated, if the body rotates about a
horizontal axis which subtends an angle 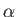 with the
with the  -axis then
-axis then
 |
(2.35) |
where
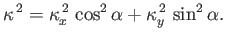 |
(2.36) |
Thus, the minimum value of
 is the lesser of
is the lesser of
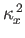 and
and
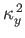 . It follows that
the equilibrium state in question is unconditionally stable provided it is stable to small
amplitude angular displacements about horizontal axes normal to its two vertical symmetry planes (i.e., the
. It follows that
the equilibrium state in question is unconditionally stable provided it is stable to small
amplitude angular displacements about horizontal axes normal to its two vertical symmetry planes (i.e., the  and
and
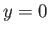 planes).
planes).
As an example, consider a uniform rectangular block of specific gravity  floating such that its sides
of length
floating such that its sides
of length 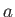 ,
,  , and
, and 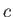 are parallel to the
are parallel to the  -,
-,  -, and
-, and  -axes, respectively. Such a block can be
thought of as a very crude model of a ship.
The volume of the
block is
-axes, respectively. Such a block can be
thought of as a very crude model of a ship.
The volume of the
block is 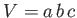 . Hence, the submerged volume is
. Hence, the submerged volume is
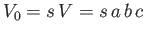 . The cross-sectional
area of the block at the waterline (
. The cross-sectional
area of the block at the waterline ( ) is
) is 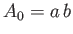 .
It is easily demonstrated that
.
It is easily demonstrated that
 . Thus, the center of buoyancy lies a depth
. Thus, the center of buoyancy lies a depth
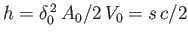 below
the surface of the water. [See Equation (2.25).] Moreover, by symmetry, the center of gravity is a height
below
the surface of the water. [See Equation (2.25).] Moreover, by symmetry, the center of gravity is a height 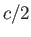 above the bottom surface of the block, which is located
a depth
above the bottom surface of the block, which is located
a depth 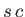 below the surface of the water. Hence,
below the surface of the water. Hence,
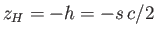 ,
,
 , and
, and
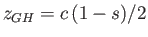 . Consider the
stability of the block to small amplitude angular displacements about the
. Consider the
stability of the block to small amplitude angular displacements about the  -axis. We have
-axis. We have
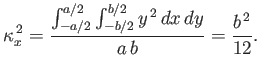 |
(2.37) |
Hence, from Equation (2.32), the metacentric height is
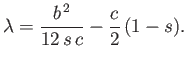 |
(2.38) |
The stability criterion 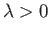 yields
yields
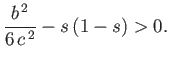 |
(2.39) |
Because the maximum value that 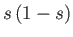 can take is
can take is 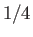 , it follows that the block is stable for all
specific gravities when
, it follows that the block is stable for all
specific gravities when
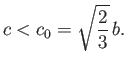 |
(2.40) |
On the other hand, if 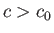 then the block is unstable for intermediate specific gravities such that
then the block is unstable for intermediate specific gravities such that
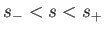 , where
, where
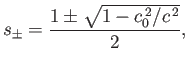 |
(2.41) |
and is stable otherwise.
Assuming that the block is stable, its angular equation of motion is written
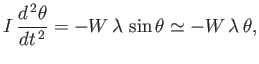 |
(2.42) |
where
![$\displaystyle I = \frac{W}{g\,V}\int_{-a/2}^{a/2}\int_{-b/2}^{b/2}\int_{-s\,c}^...
...,dx\,dy\,dz= \frac{W}{12\,g}\left(b^{\,2}+ 4\,[(1-s)^3+s^{\,3}]\,c^{\,2}\right)$](img684.png) |
(2.43) |
is the moment of inertia of the block about the  -axis. Thus, we obtain the the simple harmonic equation
-axis. Thus, we obtain the the simple harmonic equation
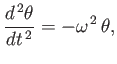 |
(2.44) |
where
![$\displaystyle \omega^{\,2} = \frac{W\,\lambda}{I}= \frac{g}{s\,c}\,\frac{c_0^{\,2}-4\,s\,(1-s)\,c^{\,2}}{c_0^{\,2}+(8/3)\,[(1-s)^3+s^{\,3}]\,c^{\,2}}.$](img686.png) |
(2.45) |
We conclude that the block executes small amplitude angular oscillations about the  -axis at the angular frequency
-axis at the angular frequency 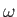 . For the case of rotation about the
. For the case of rotation about the  -axis, the previous analysis
is unchanged except that
-axis, the previous analysis
is unchanged except that
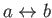 . The previous analysis again neglects the phenomenon of added mass, and, therefore,
underestimates the effective inertia of the block. (See Sections 5.9 and 7.10.)
. The previous analysis again neglects the phenomenon of added mass, and, therefore,
underestimates the effective inertia of the block. (See Sections 5.9 and 7.10.)
The metacentric height of a conventional ship whose length greatly exceeds its width is typically
much less for rolling (i.e., rotation about a horizontal axis
running along the ship's length) than for pitching (i.e., rotation about a horizontal axis
perpendicular to the ship's length), because the radius of gyration for pitching greatly exceeds that for rolling.
As is clear
from Equation (2.45), a ship with a relatively small metacentric height (for rolling) has a relatively long roll period, and vice versa. An excessively low metacentric height increases the chances of a ship capsizing if the weather is rough, if its cargo/ballast shifts, or if the ship is
damaged and partially flooded. For this reason, maritime regulatory agencies, such as the International Maritime Organization, specify minimum metacentric heights for various different types of sea-going vessel. A relatively large metacentric height, on the other hand,
generally renders a ship uncomfortable for passengers and crew, because the ship executes short period rolls, resulting in large g-forces. Such forces also increase the risk that cargo may break loose or shift.
We saw earlier, in Section 2.4, that if a body of specific gravity  floats in vertical equilibrium in a certain position
then a body of the same shape, but of specific gravity
floats in vertical equilibrium in a certain position
then a body of the same shape, but of specific gravity 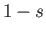 , can float in vertical equilibrium in the inverted position. We shall now
demonstrate that these positions are either both stable, or both unstable, provided the body is
of uniform density. Let
, can float in vertical equilibrium in the inverted position. We shall now
demonstrate that these positions are either both stable, or both unstable, provided the body is
of uniform density. Let  and
and 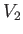 be
the volumes that are above and below the waterline, respectively, in the first position. Let
be
the volumes that are above and below the waterline, respectively, in the first position. Let 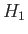 and
and
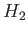 be the mean centers of these two volumes, and
be the mean centers of these two volumes, and 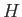 that of the whole volume. It follows that
that of the whole volume. It follows that
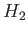 is the center of buoyancy in the first position,
is the center of buoyancy in the first position, 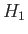 the center of buoyancy in the second (inverted) position, and
the center of buoyancy in the second (inverted) position, and
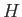 the center of gravity in both positions. Moreover,
the center of gravity in both positions. Moreover,
 |
(2.46) |
where 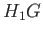 is the distance between points
is the distance between points 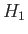 and
and 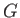 , et cetera.
The metacentric heights in the first and second positions are
, et cetera.
The metacentric heights in the first and second positions are
respectively,
where 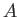 and
and 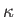 are the area and radius of gyration of the common waterline section, respectively.
Thus,
are the area and radius of gyration of the common waterline section, respectively.
Thus,
![$\displaystyle \lambda_1\,\lambda_2 = \frac{1}{V_1\,V_2}\left[A\,\kappa^{\,2}- \left(\frac{V_1\,V_2}{V_1+V_2}\right) H_1H_2\right]^{\,2}\geq 0,$](img698.png) |
(2.49) |
which implies that
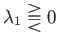 as
as
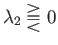 , and vice versa. It follows that the first
and second positions are either both stable, both marginally stable, or both unstable.
, and vice versa. It follows that the first
and second positions are either both stable, both marginally stable, or both unstable.



Next: Energy of a Floating
Up: Hydrostatics
Previous: Angular Stability of Floating
Richard Fitzpatrick
2016-01-22
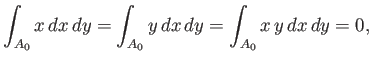
![$\displaystyle \delta_0 = \left[\frac{\int_{A_0}\delta^{\,2}(x,y)\,dx\,dy}{A_0}\right]^{1/2}.$](img634.png)
![]() about the
about the ![]() -axis.
As is easily demonstrated, the body's new draft becomes
-axis.
As is easily demonstrated, the body's new draft becomes
![]() . Hence, the new submerged volume is
. Hence, the new submerged volume is
![$\displaystyle V_0'=\int_{A_0} [\delta(x,y) -\theta\,y]\,dx\,dy = V_0 + \theta\int_{A_0} y\,dx\,dy = V_0,$](img637.png)
![$\displaystyle h' = \frac{\int_{A_0}\int_0^{\delta'} z\,dx\,dy\,dz}{V_0}=\frac{1...
...\,2}(x,y) -2\,\theta\,y\,\delta(x,y) + {\cal O}(\theta^{\,2})\right]dx\,dy = h,$](img638.png)
![$\displaystyle \frac{\int_{A_0}\int_0^{\delta'}y\,dx\,dy\,dz}{V_0}=\frac{\int_{A...
...[\delta(x,y)-\theta\,y]\,dx\,dy}{V_0}=-\theta\,\frac{\kappa_x^{\,2}\,A_0}{V_0},$](img639.png)
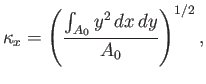
![]() about the
about the ![]() -axis then its center of buoyancy shifts horizontally a distance
-axis then its center of buoyancy shifts horizontally a distance
![]() in the plane perpendicular to the axis of rotation.
In other words, the distance
in the plane perpendicular to the axis of rotation.
In other words, the distance ![]() in Figure 2.1 is
in Figure 2.1 is
![]() . Simple trigonometry
reveals that
. Simple trigonometry
reveals that
![]() (assuming that
(assuming that ![]() is small). Hence,
is small). Hence,
![]() . Now,
. Now, ![]() is the height of the metacenter
relative to the center of buoyancy. However, the center of buoyancy lies a depth
is the height of the metacenter
relative to the center of buoyancy. However, the center of buoyancy lies a depth ![]() below the surface of the water (which corresponds to the plane
below the surface of the water (which corresponds to the plane ![]() ).
Hence, the
).
Hence, the ![]() -coordinate of the metacenter is
-coordinate of the metacenter is
![]() . Finally, if
. Finally, if ![]() and
and ![]() are the
are the ![]() -coordinates of the unperturbed
centers of gravity and buoyancy, respectively, then
-coordinates of the unperturbed
centers of gravity and buoyancy, respectively, then
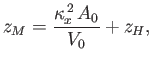
![]() about the
about the ![]() -axis then the metacentric height is
-axis then the metacentric height is



![]() floating such that its sides
of length
floating such that its sides
of length ![]() ,
, ![]() , and
, and ![]() are parallel to the
are parallel to the ![]() -,
-, ![]() -, and
-, and ![]() -axes, respectively. Such a block can be
thought of as a very crude model of a ship.
The volume of the
block is
-axes, respectively. Such a block can be
thought of as a very crude model of a ship.
The volume of the
block is ![]() . Hence, the submerged volume is
. Hence, the submerged volume is
![]() . The cross-sectional
area of the block at the waterline (
. The cross-sectional
area of the block at the waterline (![]() ) is
) is ![]() .
It is easily demonstrated that
.
It is easily demonstrated that
![]() . Thus, the center of buoyancy lies a depth
. Thus, the center of buoyancy lies a depth
![]() below
the surface of the water. [See Equation (2.25).] Moreover, by symmetry, the center of gravity is a height
below
the surface of the water. [See Equation (2.25).] Moreover, by symmetry, the center of gravity is a height ![]() above the bottom surface of the block, which is located
a depth
above the bottom surface of the block, which is located
a depth ![]() below the surface of the water. Hence,
below the surface of the water. Hence,
![]() ,
,
![]() , and
, and
![]() . Consider the
stability of the block to small amplitude angular displacements about the
. Consider the
stability of the block to small amplitude angular displacements about the ![]() -axis. We have
-axis. We have
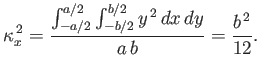
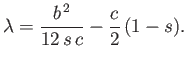
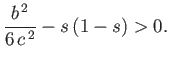
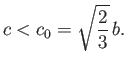
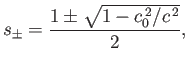
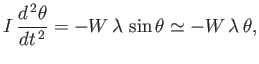
![$\displaystyle I = \frac{W}{g\,V}\int_{-a/2}^{a/2}\int_{-b/2}^{b/2}\int_{-s\,c}^...
...,dx\,dy\,dz= \frac{W}{12\,g}\left(b^{\,2}+ 4\,[(1-s)^3+s^{\,3}]\,c^{\,2}\right)$](img684.png)
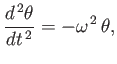
![]() floats in vertical equilibrium in a certain position
then a body of the same shape, but of specific gravity
floats in vertical equilibrium in a certain position
then a body of the same shape, but of specific gravity ![]() , can float in vertical equilibrium in the inverted position. We shall now
demonstrate that these positions are either both stable, or both unstable, provided the body is
of uniform density. Let
, can float in vertical equilibrium in the inverted position. We shall now
demonstrate that these positions are either both stable, or both unstable, provided the body is
of uniform density. Let ![]() and
and ![]() be
the volumes that are above and below the waterline, respectively, in the first position. Let
be
the volumes that are above and below the waterline, respectively, in the first position. Let ![]() and
and
![]() be the mean centers of these two volumes, and
be the mean centers of these two volumes, and ![]() that of the whole volume. It follows that
that of the whole volume. It follows that
![]() is the center of buoyancy in the first position,
is the center of buoyancy in the first position, ![]() the center of buoyancy in the second (inverted) position, and
the center of buoyancy in the second (inverted) position, and
![]() the center of gravity in both positions. Moreover,
the center of gravity in both positions. Moreover,

![$\displaystyle = \frac{\kappa^{\,2}\,A}{V_1} - H_1G =\frac{1}{V_1}\left[A\,\kappa^{\,2}- \left(\frac{V_1\,V_2}{V_1+V_2}\right) H_1H_2\right],$](img695.png)
![$\displaystyle = \frac{\kappa^{\,2}\,A}{V_2} - H_2G =\frac{1}{V_2}\left[A\,\kappa^{\,2}- \left(\frac{V_1\,V_2}{V_1+V_2}\right)H_1H_2\right],$](img697.png)
![$\displaystyle \lambda_1\,\lambda_2 = \frac{1}{V_1\,V_2}\left[A\,\kappa^{\,2}- \left(\frac{V_1\,V_2}{V_1+V_2}\right) H_1H_2\right]^{\,2}\geq 0,$](img698.png)