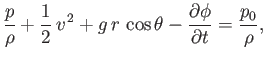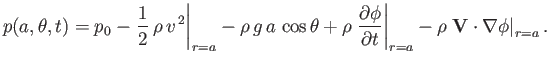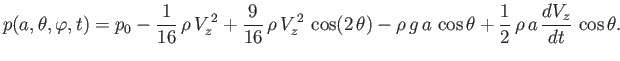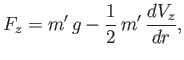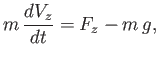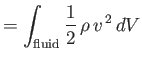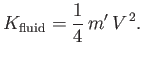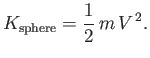Next: Conformal Maps
Up: Axisymmetric Incompressible Inviscid Flow
Previous: Flow Past a Spherical
Motion of a Submerged Sphere
Consider a situation in which an impenetrable rigid sphere of radius 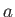 is moving through an
incompressible, inviscid fluid at the time dependent velocity
is moving through an
incompressible, inviscid fluid at the time dependent velocity
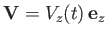 .
Assuming that the fluid and sphere were both initially stationary, it follows that the fluid
velocity field was initially irrotational. Thus, according to the Kelvin circulation theorem, the
fluid velocity field remains irrotational when the sphere starts to move. Hence, we can
write
.
Assuming that the fluid and sphere were both initially stationary, it follows that the fluid
velocity field was initially irrotational. Thus, according to the Kelvin circulation theorem, the
fluid velocity field remains irrotational when the sphere starts to move. Hence, we can
write
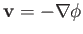 , and
, and
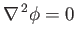 |
(7.59) |
(because the fluid is incompressible).
Let  ,
,  ,
,  be Cartesian coordinates in the initial rest frame of the fluid, and
let
be Cartesian coordinates in the initial rest frame of the fluid, and
let 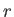 ,
, 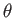 ,
, 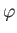 be spherical coordinates in a frame of reference that co-moves
with the sphere. In the following, all calculations are performed in the rest frame.
We expect the flow pattern set up around the sphere to be axisymmetric (i.e., independent of
be spherical coordinates in a frame of reference that co-moves
with the sphere. In the following, all calculations are performed in the rest frame.
We expect the flow pattern set up around the sphere to be axisymmetric (i.e., independent of 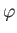 .)
We also expect the fluid a long way from the sphere to remain stationary. In other words,
.)
We also expect the fluid a long way from the sphere to remain stationary. In other words,
Moreover, because the sphere is impenetrable, we require that
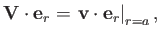 |
(7.61) |
or
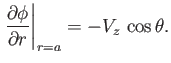 |
(7.62) |
It is easily demonstrated that the solution to Equation (7.59), subject to the
boundary conditions (7.60) and (7.62), is
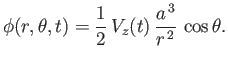 |
(7.63) |
Hence,
The general form of Bernoulli's theorem, (4.96), which applies to an irrotational flow field, yields
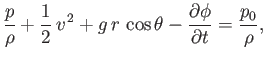 |
(7.66) |
where  is the uniform fluid mass density,
is the uniform fluid mass density, 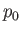 the fluid pressure at infinity, and it
is assumed that fluid and cylinder are both situated in a gravitational field of uniform acceleration
the fluid pressure at infinity, and it
is assumed that fluid and cylinder are both situated in a gravitational field of uniform acceleration
 . Thus, the
pressure distribution at the surface of the sphere can be written
. Thus, the
pressure distribution at the surface of the sphere can be written
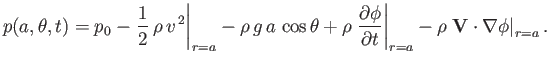 |
(7.67) |
The final term on the right-hand side of the previous equation arises because
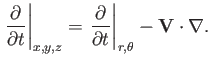 |
(7.68) |
Hence, we obtain
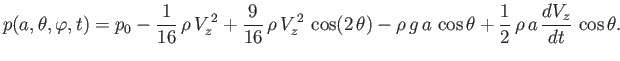 |
(7.69) |
The net force exerted on the sphere by the fluid is specified by Equations (7.55)-(7.57). It follows that
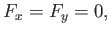 |
(7.70) |
and
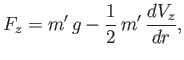 |
(7.71) |
where
 is the mass of the fluid displaced by the sphere.
The equation of vertical (i.e., in the
is the mass of the fluid displaced by the sphere.
The equation of vertical (i.e., in the  -direction) motion of the sphere is thus,
-direction) motion of the sphere is thus,
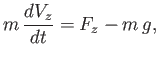 |
(7.72) |
where  is the mass of the sphere. Hence,
is the mass of the sphere. Hence,
 |
(7.73) |
It follows that the sphere moves under the action of its weight, and the buoyancy force exerted on it by
the fluid (i.e., the first and second terms, respectively, on the right-hand side of the previous equation),
as if it had the virtual mass
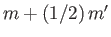 . In other words, as it moves, the sphere effectively entrains an added mass of
fluid equal to half of the displaced fluid mass. The net vertical acceleration of the sphere can
be written
. In other words, as it moves, the sphere effectively entrains an added mass of
fluid equal to half of the displaced fluid mass. The net vertical acceleration of the sphere can
be written
 |
(7.74) |
where 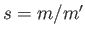 is the sphere's specific gravity. For the case of a bubble of gas in a liquid, we
expect
is the sphere's specific gravity. For the case of a bubble of gas in a liquid, we
expect 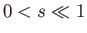 , because the gas is inevitably much less dense than the liquid. It follows that the
bubble accelerates vertically upward at twice the acceleration due to gravity.
, because the gas is inevitably much less dense than the liquid. It follows that the
bubble accelerates vertically upward at twice the acceleration due to gravity.
The origin of the sphere's added mass is easily explained. According to Equations (7.64) and (7.65),
the total kinetic energy of the fluid surrounding the sphere is
which reduces to
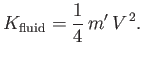 |
(7.76) |
However, the kinetic energy of the sphere is
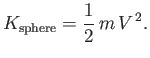 |
(7.77) |
Thus, the total kinetic energy is
 |
(7.78) |
In other words, the kinetic energy of the fluid surrounding the sphere can be accounted for by supposing that
a mass 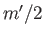 of the fluid co-moves with the sphere, and that the remainder of the fluid remains stationary.
of the fluid co-moves with the sphere, and that the remainder of the fluid remains stationary.



Next: Conformal Maps
Up: Axisymmetric Incompressible Inviscid Flow
Previous: Flow Past a Spherical
Richard Fitzpatrick
2016-01-22
![]() ,
, ![]() ,
, ![]() be Cartesian coordinates in the initial rest frame of the fluid, and
let
be Cartesian coordinates in the initial rest frame of the fluid, and
let ![]() ,
, ![]() ,
, ![]() be spherical coordinates in a frame of reference that co-moves
with the sphere. In the following, all calculations are performed in the rest frame.
We expect the flow pattern set up around the sphere to be axisymmetric (i.e., independent of
be spherical coordinates in a frame of reference that co-moves
with the sphere. In the following, all calculations are performed in the rest frame.
We expect the flow pattern set up around the sphere to be axisymmetric (i.e., independent of ![]() .)
We also expect the fluid a long way from the sphere to remain stationary. In other words,
.)
We also expect the fluid a long way from the sphere to remain stationary. In other words,