


Next: Wind Driven Waves in
Up: Waves in Incompressible Fluids
Previous: Capillary Waves
Consider a layer of fluid of density 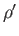 , depth
, depth  , and uniform horizontal velocity
, and uniform horizontal velocity 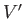 , situated on top of a layer of another fluid of density
, situated on top of a layer of another fluid of density  ,
depth
,
depth 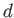 , and uniform horizontal velocity
, and uniform horizontal velocity  . Suppose that the fluids are bounded from above and below by rigid horizontal planes. Let these
planes be at
. Suppose that the fluids are bounded from above and below by rigid horizontal planes. Let these
planes be at 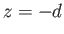 and
and 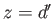 , and let the unperturbed interface between the two fluids be at
, and let the unperturbed interface between the two fluids be at  . Suppose that the elevation of the perturbed interface is
. Suppose that the elevation of the perturbed interface is 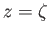 , where
, where
 .
Finally, let
.
Finally, let 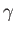 be the surface tension of the
interface. Equations (11.97), (11.98), and (11.118) yield the dispersion relation
be the surface tension of the
interface. Equations (11.97), (11.98), and (11.118) yield the dispersion relation
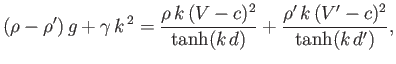 |
(11.132) |
which is a generalization of the dispersion relation (11.100) that takes surface tension into account. Here,
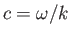 is
the phase velocity of a wave propagating along the interface.
is
the phase velocity of a wave propagating along the interface.
For the case in which both fluids are at rest, and of infinite depth, the previous dispersion relation simplifies to give
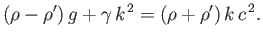 |
(11.133) |
Suppose that
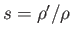 is the specific gravity of the upper fluid with respect to the lower. In the case in which
is the specific gravity of the upper fluid with respect to the lower. In the case in which 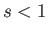 (i.e.,
the upper fluid is lighter than the lower one), it is helpful to define
(i.e.,
the upper fluid is lighter than the lower one), it is helpful to define
It follows that
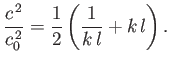 |
(11.136) |
Thus, we conclude that the phase velocity of a wave propagating along the interface between the two fluids achieves its minimum value, 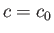 , when
, when 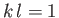 . Furthermore, waves of all wavelength
are able to propagate along the interface (i.e.,
. Furthermore, waves of all wavelength
are able to propagate along the interface (i.e.,  for all
for all 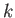 ). In the opposite case, in which
). In the opposite case, in which 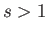 (i.e.,
the upper fluid is heavier than the lower one), we can redefine the capillary length as
(i.e.,
the upper fluid is heavier than the lower one), we can redefine the capillary length as
![$\displaystyle l = \left[\frac{\gamma}{\rho\,g\,(s-1)}\right]^{1/2}.$](img4178.png) |
(11.137) |
The dispersion relation (11.133) then becomes
 |
(11.138) |
It is apparent that 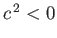 for
for  , indicating instability of the interface for waves whose wavelengths exceed the
critical value
, indicating instability of the interface for waves whose wavelengths exceed the
critical value
 . On the other hand, waves whose wavelengths are less than the critical
value are stabilized by surface tension. This result is exemplified by the experiment in which water is retained by atmospheric
pressure in an inverted glass whose mouth is closed by a gauze of fine mesh (the purpose of which is to put an upper limit on
the wavelengths of waves that can exist at the interface.)
. On the other hand, waves whose wavelengths are less than the critical
value are stabilized by surface tension. This result is exemplified by the experiment in which water is retained by atmospheric
pressure in an inverted glass whose mouth is closed by a gauze of fine mesh (the purpose of which is to put an upper limit on
the wavelengths of waves that can exist at the interface.)



Next: Wind Driven Waves in
Up: Waves in Incompressible Fluids
Previous: Capillary Waves
Richard Fitzpatrick
2016-01-22
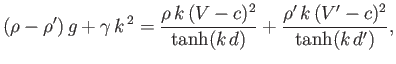
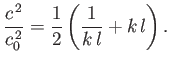
![$\displaystyle l = \left[\frac{\gamma}{\rho\,g\,(s-1)}\right]^{1/2}.$](img4178.png)
