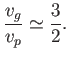Next: Capillary Waves at an
Up: Waves in Incompressible Fluids
Previous: Surface Tension
In the deep water limit  , the dispersion relation (11.121) simplifies to
, the dispersion relation (11.121) simplifies to
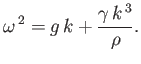 |
(11.122) |
It is helpful to introduce the capillary length,
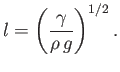 |
(11.123) |
(See Section 3.4.) The capillary length of an air/water interface at s.t.p. is
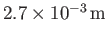 (Batchelor 2000).
The associated capillary wavelength is
(Batchelor 2000).
The associated capillary wavelength is
 .
Roughly speaking, surface tension is negligible for waves whose wavelengths are much larger than the
capillary wavelength, and vice versa.
It is
also helpful to introduce the critical phase velocity
.
Roughly speaking, surface tension is negligible for waves whose wavelengths are much larger than the
capillary wavelength, and vice versa.
It is
also helpful to introduce the critical phase velocity
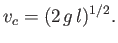 |
(11.124) |
This critical velocity takes the value
 for an air/water interface at s.t.p. (Batchelor 2000). It follows from Equation (11.122) that the phase
velocity,
for an air/water interface at s.t.p. (Batchelor 2000). It follows from Equation (11.122) that the phase
velocity,
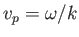 , of a surface water wave can be written
, of a surface water wave can be written
![$\displaystyle \frac{v_p}{v_c} = \left[\frac{1}{2}\left(k\,l+\frac{1}{k\,l}\right)\right]^{1/2}.$](img4150.png) |
(11.125) |
Moreover, the ratio of the phase velocity to the group velocity,
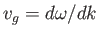 , becomes
, becomes
![$\displaystyle \frac{v_g}{v_p} =\frac{1}{2}\left[\frac{1+3\,(k\,l)^2}{1+(k\,l)^2}\right].$](img4152.png) |
(11.126) |
In the long wavelength limit
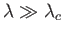 (i.e.,
(i.e.,  ), we obtain
), we obtain
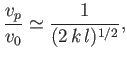 |
(11.127) |
and
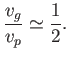 |
(11.128) |
We can identify this type of wave as the deep water gravity wave discussed in Section 11.3.
In the
short wavelength limit
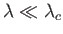 (i.e.,
(i.e., 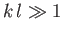 ), we get
), we get
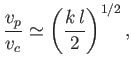 |
(11.129) |
and
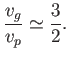 |
(11.130) |
This corresponds to a completely new type of wave known as a capillary wave. Such waves have wavelengths
that are much less than the capillary wavelength. Moreover, Equation (11.129) can be rewritten
 |
(11.131) |
which demonstrates that gravity plays no role in the propagation of a capillary wave. In fact, its place is taken by surface tension.
Finally, it is easily seen that the phase velocity (11.125) attains the minimum value  when
when
 (i.e.,
when
(i.e.,
when 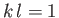 ). Moreover, from Equation (11.126),
). Moreover, from Equation (11.126), 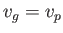 at this
wavelength. It follows that the phase velocity of a surface wave propagating over a body of water can never be less than the critical value,
at this
wavelength. It follows that the phase velocity of a surface wave propagating over a body of water can never be less than the critical value, 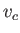 .
.



Next: Capillary Waves at an
Up: Waves in Incompressible Fluids
Previous: Surface Tension
Richard Fitzpatrick
2016-01-22
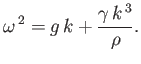
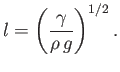
![]() (i.e.,
(i.e., ![]() ), we obtain
), we obtain
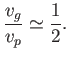
![]() (i.e.,
(i.e., ![]() ), we get
), we get