


Next: The fast Fourier transform
Up: Poisson's equation
Previous: 2-d problem with Dirichlet
2-d problem with Neumann boundary conditions
Let us redo the above calculation, replacing the Dirichlet boundary conditions (149)
with the following simple Neumann boundary conditions:
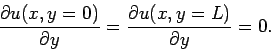 |
(161) |
In this case, we can express 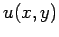 in the form
in the form
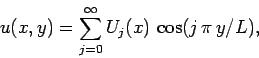 |
(162) |
which automatically satisfies the boundary conditions in the  -direction. Likewise,
we can write the source term
-direction. Likewise,
we can write the source term 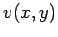 as
as
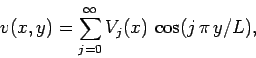 |
(163) |
where
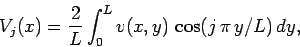 |
(164) |
since
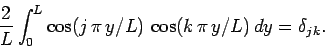 |
(165) |
Finally, the boundary conditions in the  -direction become
-direction become
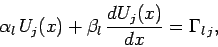 |
(166) |
at 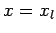 , and
, and
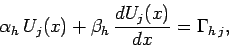 |
(167) |
at 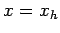 , where
, where
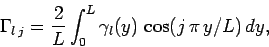 |
(168) |
etc. Note, however, that the factor in front of the integrals in Eqs. (164)
and (168) takes the special value 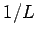 for the
for the 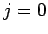 harmonic.
harmonic.
As before, we truncate the Fourier expansion in the  -direction, and discretize in the
-direction, and discretize in the
 -direction, to obtain the set of tridiagonal matrix equations specified in Eqs. (158), (159), and (160). We can solve these equations to obtain the
-direction, to obtain the set of tridiagonal matrix equations specified in Eqs. (158), (159), and (160). We can solve these equations to obtain the  , and then reconstruct
the
, and then reconstruct
the 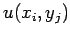 from Eq. (162). Hence, we have solved the problem.
from Eq. (162). Hence, we have solved the problem.



Next: The fast Fourier transform
Up: Poisson's equation
Previous: 2-d problem with Dirichlet
Richard Fitzpatrick
2006-03-29
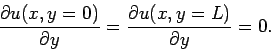
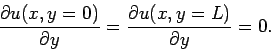
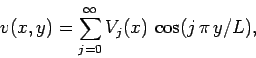
![]() -direction, and discretize in the
-direction, and discretize in the
![]() -direction, to obtain the set of tridiagonal matrix equations specified in Eqs. (158), (159), and (160). We can solve these equations to obtain the
-direction, to obtain the set of tridiagonal matrix equations specified in Eqs. (158), (159), and (160). We can solve these equations to obtain the ![]() , and then reconstruct
the
, and then reconstruct
the ![]() from Eq. (162). Hence, we have solved the problem.
from Eq. (162). Hence, we have solved the problem.