The knuckleball

Probably the most entertaining pitch in baseball is the so-called ``knuckleball.'' Unlike the other types of pitch we have encountered, knuckleballs are low speed pitches (typically, 65mph) in which the ball is purposely thrown with as little spin as possible. It turns out that knuckleballs are hard to hit because they have unstable trajectories which shift from side to side in a highly unpredictable manner. How is this possible?

Suppose that a moving ball is not spinning at all, and is orientated such that one of its stitches is exposed on one side, whereas the other side is smooth. It follows, from Fig. 11, that the drag force on the smooth side of the ball is greater than that on the stitch side. Hence, the ball experiences a lateral force in the direction of the exposed stitch. Suppose, now, that the ball is rotating slowly as it moves towards the hitter. As the ball moves forward its orientation changes, and the exposed stitch shifts from side to side, giving rise to a lateral force which also shifts from side to side. Of course, if the ball is rotating sufficiently rapidly then the oscillations in the lateral force average out. However, for a slowly rotating ball these oscillations can profoundly affect the ball's trajectory.

Watts and Sawyer²³ have performed wind tunnel measurements of the lateral force acting on a baseball as a function of its angular orientation. Note that the stitches on a baseball pass any given point four times for each complete revolution of the ball about an axis passing through its centre. Hence, we expect the lateral force to exhibit four maxima and four minima as the ball is rotated once. This is exactly what Watts and Sawyer observed. For the case of a 65mph knuckleball, Giordano has extracted the following useful expression for the lateral force, as a function of angular orientation, $\varphi$, from Watts and Sawyer's data:

$$\frac{f_y}{m\,g} = G(\varphi) = 0.5\left[\sin(4\varphi) - 0.... ...arphi) + 0.08\,\sin(12\varphi)- 0.025\,\sin(16\varphi)\right].$$ (57)

The function $G(\varphi )$ is plotted in Fig. 18. Note the very rapid changes in this function in certain narrow ranges of $\varphi$.

Figure 18: The lateral force function, $G(\varphi )$, for a 65mph knuckleball.

Using the above expression, the equations of motion of a knuckleball can be written as the following set of coupled first-order o.d.e.s:

$$\frac{dx}{dt} = v_x,$$ (58)

$$\frac{dy}{dt} = v_y,$$ (59)

$$\frac{dz}{dt} = v_z,$$ (60)

$$\frac{dv_x}{dt} = - F(v)\,v\,v_x,$$ (61)

$$\frac{dv_y}{dt} = - F(v)\,v\,v_y + g\,G(\varphi),$$ (62)

$$\frac{dv_z}{dt} = -g - F(v)\,v\,v_z.$$ (63)

$$\frac{d\varphi}{dt} = \omega.$$ (64)

Note that we have added an equation of motion for the angular orientation, $\varphi$, of the ball, which is assumed to rotate at a fixed angular velocity, $\omega$, about a vertical axis. Here, we are neglecting the Magnus force, which is expected to be negligibly small for a slowly spinning pitch. Appropriate boundary conditions at $t=0$ are:

$$x(t=0) = 0,$$ (65)

$$y(t=0) = 0,$$ (66)

$$z(t=0) = 0,$$ (67)

$$v_x(t=0) = v_0\,\cos\theta$$ (68)

$$v_y(t=0) = 0,$$ (69)

$$v_z(t=0) = v_0\,\sin\theta,$$ (70)

$$\varphi(t=0) = \varphi_0,$$ (71)

where $v_0$ is the initial speed of the pitch, $\theta$ is the pitch's initial angle of elevation, and $\varphi_0$ is the ball's initial angular orientation.

The above set of equations have been solved numerically using a fixed step-length, fourth-order Runge-Kutta method. The step-length, h, is conveniently expressed as a fraction of the pitch's estimated time-of-flight, $T = l/v_0$, where $l=18.44\,{\rm m}$ is the horizontal distance between the pitcher and the hitter. Thus, 1/h is approximately the number of steps used to integrate the trajectory.

Figure 19: Numerical trajectories of knuckleballs with the same angular velocity but different initial orientations. The solid, dotted, long-dashed, and short-dashed curves show the horizontal displacement of the ball for $\varphi _0 = 0^\circ$, $22.5^\circ$, $45^\circ$, and $67.5^\circ$, respectively. The other parameters for this pitch are $v_0=65$mph, $\theta = 4^\circ$, $\omega =20$rpm, and ${\tt h}=1\times 10^{-4}$. The ball passes over the plate at $56\,mph$ about $0.69$ seconds after it is released by the pitcher. The ball rotates about $83^\circ$ whilst it is in the air.

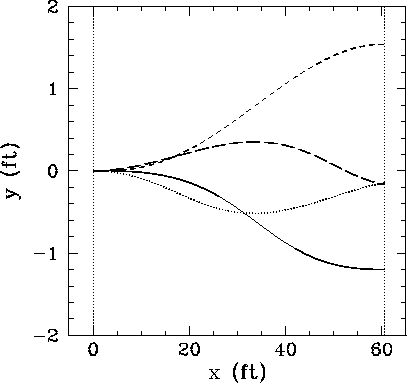Figure 19 shows the lateral displacement of a set of four knuckleballs thrown with the same rate of spin, $\omega =20$rpm, but starting with different angular orientations. Note the striking difference between the various trajectories shown in this figure. Clearly, even a fairly small change in the initial orientation of the ball translates into a large change in its subsequent trajectory through the air. For this reason, knuckleballs are extremely unpredictable--neither the pitcher, the hitter, nor the catcher can be really sure where one of these pitches is going to end up. Needless to say, baseball teams always put their best catcher behind the plate when a knuckleball pitcher is on the mound!

Figure 20: Numerical trajectory of a knuckleball. The parameters for this pitch are $v_0=65$mph, $\theta = 4^\circ$, $\varphi _0 = 0^\circ$, $\omega = 40$rpm, and ${\tt h}=1\times 10^{-4}$. The ball passes over the plate at $56\,mph$ about $0.69$ seconds after it is released by the pitcher. The ball rotates about $166^\circ$ whilst it is in the air.

Figure 20 shows the lateral displacement of a knuckleball thrown with a somewhat higher rate of spin than those shown previously: i.e., $\omega = 40$rpm. Note the curious way in which the ball ``dances'' through the air. Given that the difference between a good hit and a bad hit can correspond to a shift in the strike point on the bat by as little as $1/4$ of an inch, it must be quite a challenge to hit such a pitch well!