As is well-known, the drag force acting on an object which moves very
slowly through a viscous fluid is directly proportional to the speed
of that object with respect to the fluid. For example, a sphere
of radius ![]() , moving with speed
, moving with speed ![]() through a fluid whose coefficient of viscosity is
through a fluid whose coefficient of viscosity is ![]() ,
experiences a drag force given by Stokes' law:19
,
experiences a drag force given by Stokes' law:19
| (37) |
The origin of this second force is fairly easy to understand. At velocities
sufficiently low for Stokes' law to be valid,
air is able to flow smoothly around a passing projectile.
However, at higher velocities,
the projectile's motion is too rapid for this to occur. Instead, the projectile
effectively knocks the air out of its way. The total mass of air which the projectile comes into contact with per
second is ![]() , where
, where ![]() is the air density,
is the air density, ![]() the
projectile speed, and
the
projectile speed, and ![]() the projectile's cross-sectional area.
Suppose, as seems reasonable,
that the projectile imparts to this air mass a speed
the projectile's cross-sectional area.
Suppose, as seems reasonable,
that the projectile imparts to this air mass a speed ![]() which is directly
proportional to
which is directly
proportional to ![]() . The rate of momentum gain of the air, which is equal
to the drag force acting on the projectile, is approximately
. The rate of momentum gain of the air, which is equal
to the drag force acting on the projectile, is approximately
| (38) |
The drag force acting on a projectile, passing through air, always points in the opposite
direction to the projectile's instantaneous direction of motion. Thus, the vector
drag force takes the form
When a projectile moves through air it leaves a turbulent wake. The value of the
drag coefficient, ![]() , is closely related to the properties of this wake. Turbulence
in fluids is conventionally characterized in terms of a dimensionless quantity known
as a Reynolds number:20
, is closely related to the properties of this wake. Turbulence
in fluids is conventionally characterized in terms of a dimensionless quantity known
as a Reynolds number:20
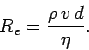 |
(40) |
Wind tunnel measurements reveal that the drag coefficient is a strong
function of speed for baseballs, as illustrated in Fig. 11.
At low speeds, the drag coefficient is approximately constant. However, as
the speed increases, ![]() drops substantially, and is more than a factor of
2 smaller at high speeds. This behaviour is similar to that described above.
The sudden drop in the drag coefficient is triggered by a transition from laminar
to turbulent flow in the air layer immediately above the ball's surface.
The critical speed (to be more exact, the critical
Reynolds number) at which this transition occurs depends on the properties of
the surface. Thus, for a completely smooth baseball the transition occurs at
speeds well beyond the capabilities of the fastest pitchers. Conversely,
the transition takes place at comparatively low speeds if the surface
of the ball is rough. In fact, the raised stitches on the otherwise smooth regulation baseball
cause the transition to occur at an intermediate speed which is
easily within the range
of major league pitchers. Note that the magnitude of the drag force is substantial--it
actually exceeds the force due to gravity for ball speeds above about 95mph.
drops substantially, and is more than a factor of
2 smaller at high speeds. This behaviour is similar to that described above.
The sudden drop in the drag coefficient is triggered by a transition from laminar
to turbulent flow in the air layer immediately above the ball's surface.
The critical speed (to be more exact, the critical
Reynolds number) at which this transition occurs depends on the properties of
the surface. Thus, for a completely smooth baseball the transition occurs at
speeds well beyond the capabilities of the fastest pitchers. Conversely,
the transition takes place at comparatively low speeds if the surface
of the ball is rough. In fact, the raised stitches on the otherwise smooth regulation baseball
cause the transition to occur at an intermediate speed which is
easily within the range
of major league pitchers. Note that the magnitude of the drag force is substantial--it
actually exceeds the force due to gravity for ball speeds above about 95mph.
 |
The above discussion leads to a number of interesting observations. First, the raised stitches on a baseball have an important influence on its aerodynamic properties. Without them, the air drag acting on the ball at high speeds would increase substantially. Indeed, it seems unlikely that major league pitchers could throw 95mph fastballs if baseballs were completely smooth. On the other hand, a scuffed-up baseball experiences even less air drag than a regulation ball. Presumably, such a ball can be thrown faster--which explains why balls are so regularly renewed in major league games.
Giordano21 has developed the following useful formula which quantifies the drag force
acting on a baseball:
| (41) |
![\begin{displaymath}
F(v) = 0.0039 + \frac{0.0058}{1+{\rm exp}[(v-v_d)/{\mit\Delta}]}.
\end{displaymath}](img364.png) |
(42) |