 |
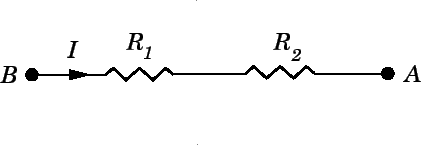
Consider two resistors connected in series, as shown in Fig. 18.
It is clear that the same current ![]() flows through both resistors.
For, if this were not the case, charge would build up in one or other
of the resistors, which would not correspond to
a steady-state situation (thus violating
the fundamental assumption of this section). Suppose that the potential drop
from point
flows through both resistors.
For, if this were not the case, charge would build up in one or other
of the resistors, which would not correspond to
a steady-state situation (thus violating
the fundamental assumption of this section). Suppose that the potential drop
from point ![]() to point
to point ![]() is
is ![]() . This drop is the sum of the potential
drops
. This drop is the sum of the potential
drops ![]() and
and ![]() across the two resistors
across the two resistors ![]() and
and ![]() , respectively.
Thus,
, respectively.
Thus,
| (135) |
| (136) |
The equivalent resistance of two resistors connected in series is the sum of the individual resistances.For
Consider two resistors connected in parallel, as shown in Fig. 19. It
is clear, from the figure, that the potential drop ![]() across the two resistors is the
same. In general, however, the currents
across the two resistors is the
same. In general, however, the currents ![]() and
and ![]() which flow
through resistors
which flow
through resistors ![]() and
and ![]() , respectively, are different.
According to Ohm's law, the equivalent resistance
, respectively, are different.
According to Ohm's law, the equivalent resistance ![]() between
between ![]() and
and ![]() is the ratio of the potential drop
is the ratio of the potential drop
![]() across these points and the current
across these points and the current ![]() which flows between them. This current must equal the sum of the
currents
which flows between them. This current must equal the sum of the
currents ![]() and
and ![]() flowing through the two resistors, otherwise
charge would build up at one or both of the junctions in the circuit.
Thus,
flowing through the two resistors, otherwise
charge would build up at one or both of the junctions in the circuit.
Thus,
| (138) |
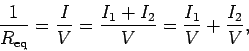 |
(139) |
The reciprocal of the equivalent resistance of two resistances connected in parallel is the sum of the reciprocals of the individual resistances.For