


Next: Capacitors in DC Circuits
Up: Electric Current
Previous: Resistors in Series and
We now know just about all that we need to know about emfs and resistors. However,
it would be convenient if we could distill our knowledge into
a number of handy rules which could then be used to analyze any DC circuit.
This is essentially what the German physicist Gustav Kirchhoff did in 1845
when he proposed two simple rules for dealing with DC circuits.
Kirchhoff's first rule applies to junction points in DC circuits (i.e.,
points at which three or more wires come together). The junction rule is:
The sum of all the currents entering any junction point is equal to
the sum of all the currents leaving that junction point.
This rule is easy to understand. As we have already remarked, if this rule
were not satisfied then charge would build up at the junction points, violating our
fundamental steady-state assumption.
Kirchhoff's second rule applies to loops in DC circuits. The loop rule is:
The algebraic sum of the changes in electric potential encountered in a
complete traversal of any closed circuit is equal to zero.
This rule is also easy to understand. We have already seen (in Sect. 5)
that zero net work is done
in slowly moving a charge 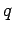 around some closed loop in an electrostatic field.
Since the work done is equal to the product of the charge
around some closed loop in an electrostatic field.
Since the work done is equal to the product of the charge 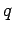 and the difference
and the difference
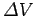 in electric potential between the beginning and end points of
the loop, it follows that this difference must be zero. Thus, if we apply this
result to the special case of a
loop in a DC circuit, we immediately arrive at Kirchhoff's second rule.
When using this rule, we first pick a closed loop in the DC circuit that
we are analyzing. Next, we decide whether we are going to traverse this
loop in a clockwise or an anti-clockwise direction (the choice is arbitrary).
If a source of emf
in electric potential between the beginning and end points of
the loop, it follows that this difference must be zero. Thus, if we apply this
result to the special case of a
loop in a DC circuit, we immediately arrive at Kirchhoff's second rule.
When using this rule, we first pick a closed loop in the DC circuit that
we are analyzing. Next, we decide whether we are going to traverse this
loop in a clockwise or an anti-clockwise direction (the choice is arbitrary).
If a source of emf 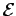 is traversed in the direction of increasing potential
then
the change in potential is
is traversed in the direction of increasing potential
then
the change in potential is 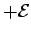 .
However, if the emf is traversed in the opposite direction then the change in potential is
.
However, if the emf is traversed in the opposite direction then the change in potential is 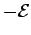 . If a resistor
. If a resistor 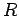 , carrying a
current
, carrying a
current  , is traversed in the direction of current flow then the change in
potential is
, is traversed in the direction of current flow then the change in
potential is 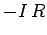 . Finally, if the resistor is traversed in the
opposite direction then the change in potential is
. Finally, if the resistor is traversed in the
opposite direction then the change in potential is 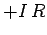 .
.
The currents flowing around a general DC circuit can always be found by applying
Kirchhoff's first rule to all junction points,
Kirchhoff's second rule to all loops, and then solving the
simultaneous algebraic equations thus obtained. This procedure works
no matter how complicated the circuit in question is (e.g., Kirchhoff's
rules are used in the semiconductor industry to analyze the incredibly
complicated circuits, etched onto the surface of silicon wafers, which are used to
construct the central processing units of computers).



Next: Capacitors in DC Circuits
Up: Electric Current
Previous: Resistors in Series and
Richard Fitzpatrick
2007-07-14