


Next: Charged Conductors
Up: Gauss' Law
Previous: Electric Field of a
Electric Field of a Uniformly Charged Plane
Consider an infinite plane which carries the uniform charge per unit area
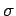 . Suppose that the plane coincides with the
. Suppose that the plane coincides with the
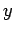 -
-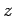 plane (i.e., the plane which satisfies
plane (i.e., the plane which satisfies  ).
By symmetry, we expect the electric field on either side of the plane to
be a function of
).
By symmetry, we expect the electric field on either side of the plane to
be a function of 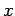 only, to be directed
normal to the plane, and to point away from/towards the plane
depending on whether
only, to be directed
normal to the plane, and to point away from/towards the plane
depending on whether 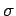 is positive/negative.
is positive/negative.
Figure 12:
The electric field generated by a uniformly charged plane.
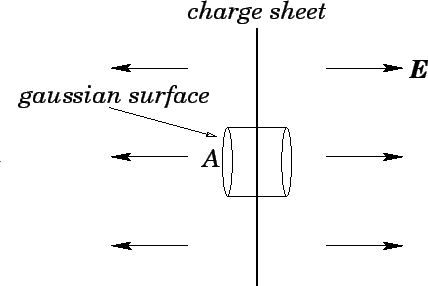 |
Let us draw a cylindrical gaussian surface, whose axis is normal
to the plane, and which is cut in half by the plane--see Fig. 12. Let the
cylinder run from 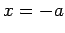 to
to 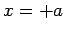 , and let its cross-sectional
area be
, and let its cross-sectional
area be  . According to Gauss' law,
. According to Gauss' law,
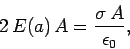 |
(72) |
where 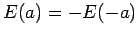 is the electric field strength at
is the electric field strength at 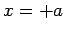 .
Here, the left-hand side represents the electric flux out of the surface. Note that the
only contributions to this flux come from the flat surfaces at the two ends of the cylinder.
The right-hand side represents the charge enclosed by the cylindrical
surface, divided by
.
Here, the left-hand side represents the electric flux out of the surface. Note that the
only contributions to this flux come from the flat surfaces at the two ends of the cylinder.
The right-hand side represents the charge enclosed by the cylindrical
surface, divided by  . It follows that
. It follows that
 |
(73) |
Note that the electric field is uniform (i.e., it does not
depend on 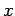 ), normal to the charged plane,
and oppositely directed on either side of the plane. The electric field always
points away from a positively charged plane, and vice versa.
), normal to the charged plane,
and oppositely directed on either side of the plane. The electric field always
points away from a positively charged plane, and vice versa.
Figure 13:
The electric field generated by two oppositely charged parallel
planes.
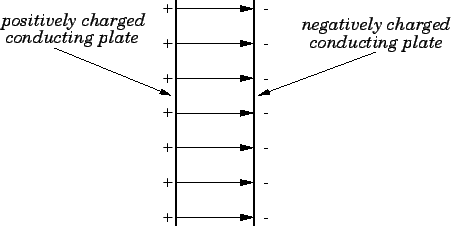 |
Consider the electric field produced by two parallel planes which carry equal
and opposite uniform charge densities 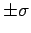 . We can calculate this field
by superposing the electric
fields produced by each plane taken in isolation. It is easily seen,
from the above discussion, that in the region between
the planes the field is uniform, normal to the planes, directed from the
positively to the negatively charged plane, and of magnitude
. We can calculate this field
by superposing the electric
fields produced by each plane taken in isolation. It is easily seen,
from the above discussion, that in the region between
the planes the field is uniform, normal to the planes, directed from the
positively to the negatively charged plane, and of magnitude
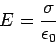 |
(74) |
--see Fig. 13.
Outside this region, the electric field cancels to zero.
The above result is only valid for two charged planes of infinite extent. However,
the result is approximately valid for two charged planes of finite extent, provided
that the spacing between the planes is small compared to their typical dimensions.



Next: Charged Conductors
Up: Gauss' Law
Previous: Electric Field of a
Richard Fitzpatrick
2007-07-14

![]() to
to ![]() , and let its cross-sectional
area be
, and let its cross-sectional
area be ![]() . According to Gauss' law,
. According to Gauss' law,