


Next: Electric Field of a
Up: Gauss' Law
Previous: Electric Field of a
Consider a long straight wire which carries the uniform
charge per unit length 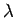 .
We expect the electric field generated by such a charge distribution
to possess cylindrical symmetry. We also expect the field to
point radially (in a cylindrical
sense) away from the wire (assuming that the wire is positively
charged).
.
We expect the electric field generated by such a charge distribution
to possess cylindrical symmetry. We also expect the field to
point radially (in a cylindrical
sense) away from the wire (assuming that the wire is positively
charged).
Figure 11:
The electric field generated by a uniformly charged wire.
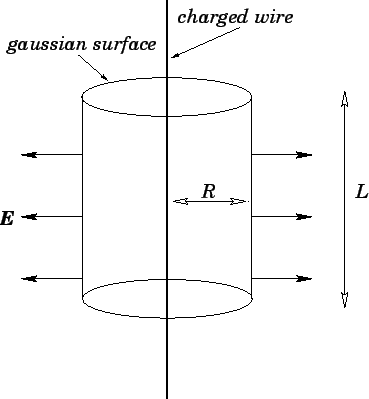 |
Let us draw a cylindrical gaussian surface, co-axial with the wire, of radius
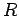 and length
and length  --see Fig. 11. The above symmetry arguments imply that the electric field generated by the wire is everywhere perpendicular
to the curved surface of the cylinder. Thus, according to Gauss' law,
--see Fig. 11. The above symmetry arguments imply that the electric field generated by the wire is everywhere perpendicular
to the curved surface of the cylinder. Thus, according to Gauss' law,
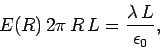 |
(70) |
where 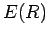 is the electric field-strength a perpendicular distance
is the electric field-strength a perpendicular distance 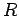 from the wire. Here, the
left-hand side represents the electric flux through the gaussian surface.
Note that there is no contribution from the two flat ends of the cylinder, since the
field is parallel to the surface there. The right-hand side represents the
total charge enclosed by the cylinder, divided by
from the wire. Here, the
left-hand side represents the electric flux through the gaussian surface.
Note that there is no contribution from the two flat ends of the cylinder, since the
field is parallel to the surface there. The right-hand side represents the
total charge enclosed by the cylinder, divided by  . It follows
that
. It follows
that
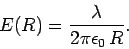 |
(71) |
The field points radially (in a cylindrical sense) away from the wire
if 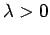 , and radially towards the wire if
, and radially towards the wire if 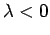 .
.



Next: Electric Field of a
Up: Gauss' Law
Previous: Electric Field of a
Richard Fitzpatrick
2007-07-14

![]() and length
and length ![]() --see Fig. 11. The above symmetry arguments imply that the electric field generated by the wire is everywhere perpendicular
to the curved surface of the cylinder. Thus, according to Gauss' law,
--see Fig. 11. The above symmetry arguments imply that the electric field generated by the wire is everywhere perpendicular
to the curved surface of the cylinder. Thus, according to Gauss' law,