Under certain circumstances (see the following section), a ship traveling over a body of water leaves behind it a train of gravity waves whose wavefronts are transverse to the ship's direction of motion. Because these waves possess energy
that is carried away from the ship, and eventually dissipated, this energy must have been produced at the ship's expense. The ship consequently experiences a drag force, 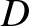 (Lamb 1932). Suppose that the ship is moving at the constant velocity
(Lamb 1932). Suppose that the ship is moving at the constant velocity 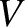 . We would
expect the transverse waves making up the train to have a matching phase velocity, so that they maintain a constant phase relation
with respect to the ship. To be more exact, we would generally expect the ship's bow to always correspond to a wave maximum (because of the
pile up of water in front of the bow produced by the ship's forward motion).
The condition
. We would
expect the transverse waves making up the train to have a matching phase velocity, so that they maintain a constant phase relation
with respect to the ship. To be more exact, we would generally expect the ship's bow to always correspond to a wave maximum (because of the
pile up of water in front of the bow produced by the ship's forward motion).
The condition 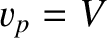 , combined with Equation (9.284), yields
, combined with Equation (9.284), yields
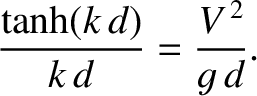 |
(9.299) |
Suppose, for the sake of argument, that the wave train is of uniform transverse width 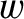 . Consider a fixed line drawn
downstream of the ship at right-angles to its path. The rate at which the length of the train is
increasing ahead of this line is
. Consider a fixed line drawn
downstream of the ship at right-angles to its path. The rate at which the length of the train is
increasing ahead of this line is 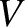 . Therefore, the rate at which the energy of the train is increasing ahead of the
line is
. Therefore, the rate at which the energy of the train is increasing ahead of the
line is
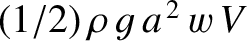 , where
, where 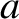 is the typical amplitude of the transverse waves in the train. As is readily demonstrated [and
is evident from Equation (9.35)], wave
energy travels at the group velocity, rather than the phase velocity (Lighthill 1978). Thus, the energy flux per unit width of a propagating gravity wave is
simply
is the typical amplitude of the transverse waves in the train. As is readily demonstrated [and
is evident from Equation (9.35)], wave
energy travels at the group velocity, rather than the phase velocity (Lighthill 1978). Thus, the energy flux per unit width of a propagating gravity wave is
simply 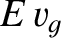 . Wave energy consequently crosses our fixed line in the direction of the ship's motion at the
rate
. Wave energy consequently crosses our fixed line in the direction of the ship's motion at the
rate
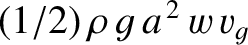 . Finally, the ship does work against the drag force, which goes to increase the energy of the train in the
region ahead of our line, at the rate
. Finally, the ship does work against the drag force, which goes to increase the energy of the train in the
region ahead of our line, at the rate 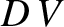 . Energy conservation thus yields
. Energy conservation thus yields
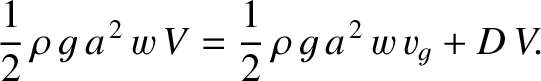 |
(9.300) |
However, because 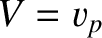 , we obtain
, we obtain
![$\displaystyle D = \frac{1}{2}\,\,\rho\,g\,a^{\,2}\,w\left(1-\frac{v_g}{v_p}\right)=\frac{1}{4}\,\rho\,g\,a^{\,2}\,w\left[1-\frac{2\,k\,d}{\sinh(2\,k\,d)}\right],$](img3082.png) |
(9.301) |
where use has been made of Equation (9.285).
Here, 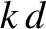 is determined implicitly in terms of the ship speed via Equation (9.299). However, this equation
cannot be satisfied when the speed exceeds the critical value
is determined implicitly in terms of the ship speed via Equation (9.299). However, this equation
cannot be satisfied when the speed exceeds the critical value
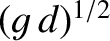 , because gravity waves cannot
propagate at speeds in excess of this value. In this situation, no transverse wave train can keep up with the ship, and the drag associated with such waves consequently disappears. In fact, we can see, from the previous formulae, that when
, because gravity waves cannot
propagate at speeds in excess of this value. In this situation, no transverse wave train can keep up with the ship, and the drag associated with such waves consequently disappears. In fact, we can see, from the previous formulae, that when
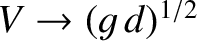 then
then
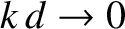 , and so
, and so
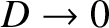 . Actually, the transverse wave amplitude,
. Actually, the transverse wave amplitude, 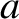 , generally increases
significantly as the ship speed approaches the critical value. Hence, the drag due to transverse waves actually peaks strongly at speeds just below the critical speed,
before effectively falling to zero as this speed is exceeded. Consequently, it usually requires a
great deal of propulsion power to force a ship to travel at speeds faster than
, generally increases
significantly as the ship speed approaches the critical value. Hence, the drag due to transverse waves actually peaks strongly at speeds just below the critical speed,
before effectively falling to zero as this speed is exceeded. Consequently, it usually requires a
great deal of propulsion power to force a ship to travel at speeds faster than
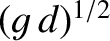 .
.
In the deep water limit 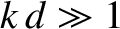 , Equation (9.301) reduces to
, Equation (9.301) reduces to
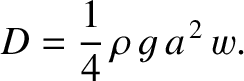 |
(9.302) |
At fixed wave amplitude, this expression is independent of the wavelength of the wave train, and, hence, independent of the
ship's speed. This result is actually rather misleading. In fact, (at fixed wave amplitude) the drag acting on a ship traveling
through deep water varies significantly with the ship's speed. We can account for
this variation by incorporating the finite length of the ship into our analysis. A real ship moving through water generates a bow wave from
its bow, and a stern wave from its stern. Moreover, the bow wave tends to have a positive vertical displacement, because water naturally piles up in front of the bow due to the forward motion of the ship,
whereas the stern wave tends to have a negative vertical displacement, because water rushes into the void left by the stern. Very roughly
speaking, suppose that the vertical displacement of the water surface caused by the ship is of the form
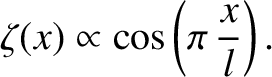 |
(9.303) |
Here, 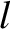 is the length of the ship. Moreover, the bow lies (instantaneously) at
is the length of the ship. Moreover, the bow lies (instantaneously) at 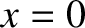 [hence,
[hence,
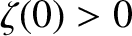 ], and the stern at
], and the stern at 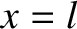 [hence,
[hence,
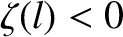 ].
For the sake of simplicity, the upward water displacement due to the bow is assumed to equal the downward displacement due to the stern.
At fixed bow wave displacement, the
amplitude of transverse gravity waves of wavenumber
].
For the sake of simplicity, the upward water displacement due to the bow is assumed to equal the downward displacement due to the stern.
At fixed bow wave displacement, the
amplitude of transverse gravity waves of wavenumber
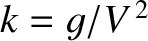 (chosen so that the phase velocity of the waves
matches the ship's speed,
(chosen so that the phase velocity of the waves
matches the ship's speed, 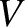 ) produced by the ship is
) produced by the ship is
![$\displaystyle a\propto \frac{1}{l}\int_0^l\cos\left(\pi\,\frac{x}{l}\right)\cos(k\,x)\,dx = \frac{1}{2}\left[{\rm sinc}(\pi-k\,l)+{\rm sinc}(\pi+k\,l)\right],$](img3093.png) |
(9.304) |
where
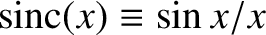 .
In other words, the amplitude is proportional to the Fourier coefficient of the ship's vertical displacement pattern evaluated for
a wavenumber that matches that of the wave train.
Hence, (at fixed bow wave displacement) the drag produced by the transverse waves is
.
In other words, the amplitude is proportional to the Fourier coefficient of the ship's vertical displacement pattern evaluated for
a wavenumber that matches that of the wave train.
Hence, (at fixed bow wave displacement) the drag produced by the transverse waves is
![$\displaystyle D\propto a^{\,2}\propto \left[{\rm sinc}\left(\pi-F^{\,-2}\right)+{\rm sinc}\left(\pi+F^{\,-2}\right)\right]^{\,2},$](img3094.png) |
(9.305) |
where the dimensionless parameter
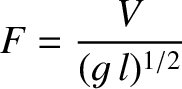 |
(9.306) |
is known as the Froude number.
Figure 9.5:
Variation of wave drag with Froude number for a ship traveling through deep water.
|
|
Figure 9.5 illustrates the variation of the wave drag with Froude number predicted by Equation (9.305).
As we can see, if the Froude number is much less than unity, which implies that the wavelength of the wave train is much smaller than the length of the
ship, then the drag is comparatively small. This is the case because the ship is extremely inefficient at driving short wavelength gravity waves.
The drag
increases as the Froude number increases, reaching a relatively sharp maximum when
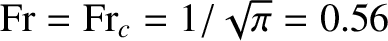 , and then falls rapidly.
When
, and then falls rapidly.
When
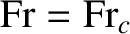 the length of the ship is equal to half the wavelength of the wave train. In this situation, the bow and stern waves interfere constructively, leading to
a particularly large amplitude wave train, and, hence, to a particularly large wave drag. The smaller peaks visible in the figure correspond to other situations
in which the bow and stern waves interfere constructively. (For instance, when the length of the ship
corresponds to one and a half wavelengths of the wave train.) A heavy ship with a large displacement, and limited propulsion
power, generally cannot overcome the peak in the wave drag that occurs when
the length of the ship is equal to half the wavelength of the wave train. In this situation, the bow and stern waves interfere constructively, leading to
a particularly large amplitude wave train, and, hence, to a particularly large wave drag. The smaller peaks visible in the figure correspond to other situations
in which the bow and stern waves interfere constructively. (For instance, when the length of the ship
corresponds to one and a half wavelengths of the wave train.) A heavy ship with a large displacement, and limited propulsion
power, generally cannot overcome the peak in the wave drag that occurs when
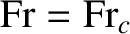 .
Such a ship is, therefore, limited to Froude numbers in the range
.
Such a ship is, therefore, limited to Froude numbers in the range
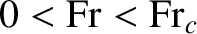 , which
implies a maximum speed of
, which
implies a maximum speed of
![$\displaystyle V_c = 0.56\,(g\,l)^{1/2} = 1.75\,[l({\rm m})]^{1/2}\,{\rm m/s} = 3.4\,[l({\rm m})]^{1/2}\,{\rm kts}.$](img3100.png) |
(9.307) |
This characteristic speed is sometimes called the hull speed. It can be seen that the hull speed increases with the length of the ship. In other words, long ships have higher
hull speeds than short ones.
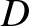 (Lamb 1932). Suppose that the ship is moving at the constant velocity
(Lamb 1932). Suppose that the ship is moving at the constant velocity 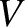 . We would
expect the transverse waves making up the train to have a matching phase velocity, so that they maintain a constant phase relation
with respect to the ship. To be more exact, we would generally expect the ship's bow to always correspond to a wave maximum (because of the
pile up of water in front of the bow produced by the ship's forward motion).
The condition
. We would
expect the transverse waves making up the train to have a matching phase velocity, so that they maintain a constant phase relation
with respect to the ship. To be more exact, we would generally expect the ship's bow to always correspond to a wave maximum (because of the
pile up of water in front of the bow produced by the ship's forward motion).
The condition 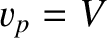 , combined with Equation (9.284), yields
Suppose, for the sake of argument, that the wave train is of uniform transverse width
, combined with Equation (9.284), yields
Suppose, for the sake of argument, that the wave train is of uniform transverse width 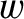 . Consider a fixed line drawn
downstream of the ship at right-angles to its path. The rate at which the length of the train is
increasing ahead of this line is
. Consider a fixed line drawn
downstream of the ship at right-angles to its path. The rate at which the length of the train is
increasing ahead of this line is 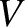 . Therefore, the rate at which the energy of the train is increasing ahead of the
line is
. Therefore, the rate at which the energy of the train is increasing ahead of the
line is
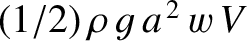 , where
, where 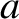 is the typical amplitude of the transverse waves in the train. As is readily demonstrated [and
is evident from Equation (9.35)], wave
energy travels at the group velocity, rather than the phase velocity (Lighthill 1978). Thus, the energy flux per unit width of a propagating gravity wave is
simply
is the typical amplitude of the transverse waves in the train. As is readily demonstrated [and
is evident from Equation (9.35)], wave
energy travels at the group velocity, rather than the phase velocity (Lighthill 1978). Thus, the energy flux per unit width of a propagating gravity wave is
simply 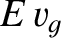 . Wave energy consequently crosses our fixed line in the direction of the ship's motion at the
rate
. Wave energy consequently crosses our fixed line in the direction of the ship's motion at the
rate
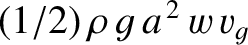 . Finally, the ship does work against the drag force, which goes to increase the energy of the train in the
region ahead of our line, at the rate
. Finally, the ship does work against the drag force, which goes to increase the energy of the train in the
region ahead of our line, at the rate 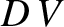 . Energy conservation thus yields
. Energy conservation thus yields
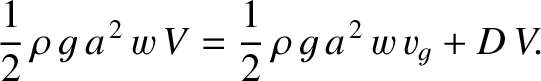
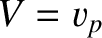 , we obtain
where use has been made of Equation (9.285).
Here,
, we obtain
where use has been made of Equation (9.285).
Here, 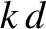 is determined implicitly in terms of the ship speed via Equation (9.299). However, this equation
cannot be satisfied when the speed exceeds the critical value
is determined implicitly in terms of the ship speed via Equation (9.299). However, this equation
cannot be satisfied when the speed exceeds the critical value
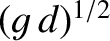 , because gravity waves cannot
propagate at speeds in excess of this value. In this situation, no transverse wave train can keep up with the ship, and the drag associated with such waves consequently disappears. In fact, we can see, from the previous formulae, that when
, because gravity waves cannot
propagate at speeds in excess of this value. In this situation, no transverse wave train can keep up with the ship, and the drag associated with such waves consequently disappears. In fact, we can see, from the previous formulae, that when
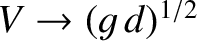 then
then
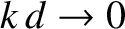 , and so
, and so
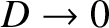 . Actually, the transverse wave amplitude,
. Actually, the transverse wave amplitude, 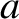 , generally increases
significantly as the ship speed approaches the critical value. Hence, the drag due to transverse waves actually peaks strongly at speeds just below the critical speed,
before effectively falling to zero as this speed is exceeded. Consequently, it usually requires a
great deal of propulsion power to force a ship to travel at speeds faster than
, generally increases
significantly as the ship speed approaches the critical value. Hence, the drag due to transverse waves actually peaks strongly at speeds just below the critical speed,
before effectively falling to zero as this speed is exceeded. Consequently, it usually requires a
great deal of propulsion power to force a ship to travel at speeds faster than
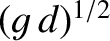 .
.
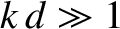 , Equation (9.301) reduces to
, Equation (9.301) reduces to
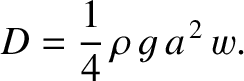
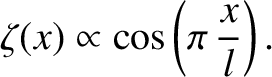
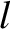 is the length of the ship. Moreover, the bow lies (instantaneously) at
is the length of the ship. Moreover, the bow lies (instantaneously) at 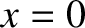 [hence,
[hence,
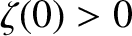 ], and the stern at
], and the stern at 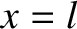 [hence,
[hence,
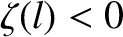 ].
For the sake of simplicity, the upward water displacement due to the bow is assumed to equal the downward displacement due to the stern.
At fixed bow wave displacement, the
amplitude of transverse gravity waves of wavenumber
].
For the sake of simplicity, the upward water displacement due to the bow is assumed to equal the downward displacement due to the stern.
At fixed bow wave displacement, the
amplitude of transverse gravity waves of wavenumber
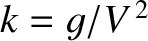 (chosen so that the phase velocity of the waves
matches the ship's speed,
(chosen so that the phase velocity of the waves
matches the ship's speed, 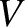 ) produced by the ship is
) produced by the ship is
![$\displaystyle a\propto \frac{1}{l}\int_0^l\cos\left(\pi\,\frac{x}{l}\right)\cos(k\,x)\,dx = \frac{1}{2}\left[{\rm sinc}(\pi-k\,l)+{\rm sinc}(\pi+k\,l)\right],$](img3093.png)
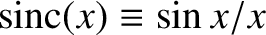 .
In other words, the amplitude is proportional to the Fourier coefficient of the ship's vertical displacement pattern evaluated for
a wavenumber that matches that of the wave train.
Hence, (at fixed bow wave displacement) the drag produced by the transverse waves is
where the dimensionless parameter
.
In other words, the amplitude is proportional to the Fourier coefficient of the ship's vertical displacement pattern evaluated for
a wavenumber that matches that of the wave train.
Hence, (at fixed bow wave displacement) the drag produced by the transverse waves is
where the dimensionless parameter
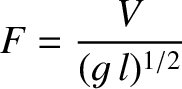
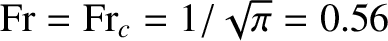 , and then falls rapidly.
When
, and then falls rapidly.
When
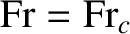 the length of the ship is equal to half the wavelength of the wave train. In this situation, the bow and stern waves interfere constructively, leading to
a particularly large amplitude wave train, and, hence, to a particularly large wave drag. The smaller peaks visible in the figure correspond to other situations
in which the bow and stern waves interfere constructively. (For instance, when the length of the ship
corresponds to one and a half wavelengths of the wave train.) A heavy ship with a large displacement, and limited propulsion
power, generally cannot overcome the peak in the wave drag that occurs when
the length of the ship is equal to half the wavelength of the wave train. In this situation, the bow and stern waves interfere constructively, leading to
a particularly large amplitude wave train, and, hence, to a particularly large wave drag. The smaller peaks visible in the figure correspond to other situations
in which the bow and stern waves interfere constructively. (For instance, when the length of the ship
corresponds to one and a half wavelengths of the wave train.) A heavy ship with a large displacement, and limited propulsion
power, generally cannot overcome the peak in the wave drag that occurs when
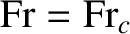 .
Such a ship is, therefore, limited to Froude numbers in the range
.
Such a ship is, therefore, limited to Froude numbers in the range
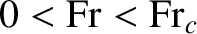 , which
implies a maximum speed of
, which
implies a maximum speed of
![$\displaystyle V_c = 0.56\,(g\,l)^{1/2} = 1.75\,[l({\rm m})]^{1/2}\,{\rm m/s} = 3.4\,[l({\rm m})]^{1/2}\,{\rm kts}.$](img3100.png)