Damped Harmonic Oscillation
Consider the mass–spring system discussed in Section 1.2.
Suppose that, as it slides over the horizontal surface, the mass is subject to
a frictional damping force that opposes its motion, and is directly
proportional to its instantaneous velocity. It follows that the net force acting
on the mass when its instantaneous displacement is  takes the form
takes the form
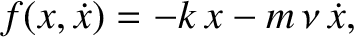 |
(2.1) |
where 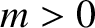 is the mass,
is the mass, 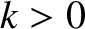 the spring force constant, and
the spring force constant, and  a constant (with the dimensions of angular frequency) that parameterizes the strength of the damping. The time evolution equation of the
system thus becomes [cf., Equation (1.2)]
a constant (with the dimensions of angular frequency) that parameterizes the strength of the damping. The time evolution equation of the
system thus becomes [cf., Equation (1.2)]
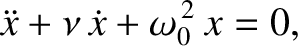 |
(2.2) |
where
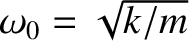 is the undamped oscillation frequency [cf., Equation (1.6)]. We shall
refer to the preceding equation as the damped harmonic oscillator equation.
is the undamped oscillation frequency [cf., Equation (1.6)]. We shall
refer to the preceding equation as the damped harmonic oscillator equation.
It is worth discussing the two forces that appear on the right-hand side of Equation (2.1) in more detail. The
first is the restoring force that develops when a mechanical system in a stable equilibrium state
is slightly disturbed from that state. We can suppose, without loss of generality, that the
equilibrium state corresponds to 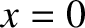 . Suppose that
. Suppose that 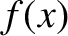 is the restoring force. It follows that
is the restoring force. It follows that
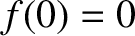 and
and
 , otherwise
, otherwise 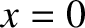 is not a stable equilibrium point. Taylor expanding about
is not a stable equilibrium point. Taylor expanding about 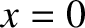 (Riley 1974), we obtain
(Riley 1974), we obtain
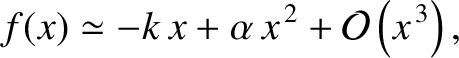 |
(2.3) |
where
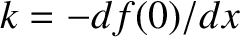 , and
, and
 . It follows that, provided the magnitude of the displacement from the
equilibrium point,
. It follows that, provided the magnitude of the displacement from the
equilibrium point, 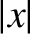 , remains sufficiently small, we can always approximate
, remains sufficiently small, we can always approximate 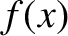 by the first non-zero term in its Taylor
expansion; that is,
by the first non-zero term in its Taylor
expansion; that is,
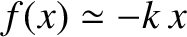 . Thus, the first term that appears on the right-hand side of Equation (2.1)
is exact (as long as the amplitude of the motion remains sufficiently small). The second term, on the other hand,
which represents the damping force, is completely phenomenological. In other words, damping forces that
arise in nature are not necessarily directly proportional to the instantaneous velocity of the system. For example,
the damping force that arises from air resistance is usually directly proportional to the square of the
instantaneous velocity (Batchelor 2000). In fact, the only reason that we have chosen a damping force that is
directly proportional to the instantaneous velocity is that it leads to a linear equation of motion.
. Thus, the first term that appears on the right-hand side of Equation (2.1)
is exact (as long as the amplitude of the motion remains sufficiently small). The second term, on the other hand,
which represents the damping force, is completely phenomenological. In other words, damping forces that
arise in nature are not necessarily directly proportional to the instantaneous velocity of the system. For example,
the damping force that arises from air resistance is usually directly proportional to the square of the
instantaneous velocity (Batchelor 2000). In fact, the only reason that we have chosen a damping force that is
directly proportional to the instantaneous velocity is that it leads to a linear equation of motion.
Let us search for a solution to Equation (2.2) of the form
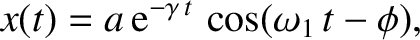 |
(2.4) |
where 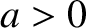 ,
, 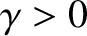 ,
,
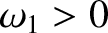 , and
, and  are all constants. By analogy
with the discussion in Section 1.2, we can interpret the
preceding solution as a periodic oscillation, of fixed angular frequency
are all constants. By analogy
with the discussion in Section 1.2, we can interpret the
preceding solution as a periodic oscillation, of fixed angular frequency 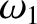 ,
and phase angle
,
and phase angle  , whose amplitude decays exponentially in
time as
, whose amplitude decays exponentially in
time as
 . It can be demonstrated that
Hence, collecting similar terms, Equation (2.2) becomes
. It can be demonstrated that
Hence, collecting similar terms, Equation (2.2) becomes
| 0 |
![$\displaystyle =\left[ \left(\gamma^{\,2}-\omega_1^{\,2}\right) -\nu\,\gamma + \omega_0^{\,2}\right]a\,{\rm e}^{-\gamma\,t}\,\cos(\omega_1\,t-\phi)$](img432.png) |
|
| |
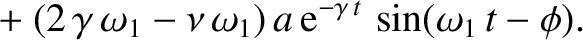 |
(2.7) |
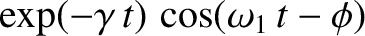 and
and
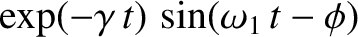 separately equate to zero, so that
These equations can be solved to give
separately equate to zero, so that
These equations can be solved to give
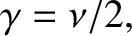 |
(2.10) |
and
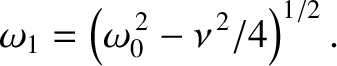 |
(2.11) |
Thus, the solution to the damped harmonic oscillator equation is written
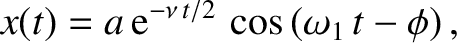 |
(2.12) |
assuming that
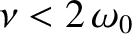 (because
(because
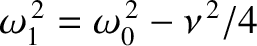 cannot be negative). We conclude that the effect of a relatively small amount of damping, parameterized
by the damping constant,
cannot be negative). We conclude that the effect of a relatively small amount of damping, parameterized
by the damping constant, 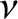 ,
on a system that exhibits simple harmonic oscillation about a stable equilibrium state is to reduce the
angular frequency of the oscillation from its undamped value
,
on a system that exhibits simple harmonic oscillation about a stable equilibrium state is to reduce the
angular frequency of the oscillation from its undamped value 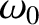 to
to
 , and to cause the amplitude of the oscillation to decay exponentially
in time at the rate
, and to cause the amplitude of the oscillation to decay exponentially
in time at the rate 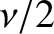 . This modified type of oscillation, which we shall refer to as damped harmonic oscillation, is illustrated in Figure 2.1.
Incidentally, if the damping is sufficiently large that
. This modified type of oscillation, which we shall refer to as damped harmonic oscillation, is illustrated in Figure 2.1.
Incidentally, if the damping is sufficiently large that
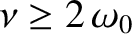 (which we shall assume not to be the case) then
the system does not oscillate at all, and any motion simply decays away exponentially
in time. (See Exercise 7.)
(which we shall assume not to be the case) then
the system does not oscillate at all, and any motion simply decays away exponentially
in time. (See Exercise 7.)
Figure 2.1:
Damped harmonic oscillation. Here,
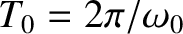 ,
,
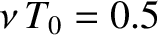 , and
, and 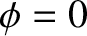 . The solid line shows
. The solid line shows 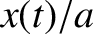 , whereas the dashed lines
show
, whereas the dashed lines
show
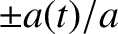 .
.
|
|
Although the angular frequency, 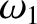 , and decay rate,
, and decay rate, 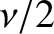 ,
of the damped harmonic oscillation specified in Equation (2.12) are determined by the constants appearing in the damped harmonic oscillator equation, (2.2), the initial amplitude,
,
of the damped harmonic oscillation specified in Equation (2.12) are determined by the constants appearing in the damped harmonic oscillator equation, (2.2), the initial amplitude,  , and the phase angle,
, and the phase angle,  ,
of the oscillation
are determined by the initial conditions. In fact, if
,
of the oscillation
are determined by the initial conditions. In fact, if 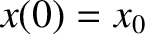 and
and
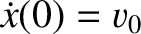 then it follows from Equation (2.12) that
then it follows from Equation (2.12) that
which implies that
giving
The damped harmonic oscillator equation is a linear differential equation. In other words, if  is a
solution then so is
is a
solution then so is 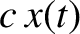 , where
, where 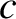 is an arbitrary constant. It follows
that the solutions of this equation are superposable,
so that if
is an arbitrary constant. It follows
that the solutions of this equation are superposable,
so that if 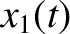 and
and 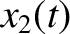 are two solutions corresponding to different initial
conditions then
are two solutions corresponding to different initial
conditions then
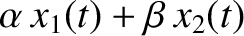 is a third solution, where
is a third solution, where 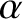 and
and 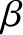 are arbitrary constants.
are arbitrary constants.
Multiplying the damped harmonic oscillator equation, (2.2), by 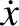 ,
we obtain
,
we obtain
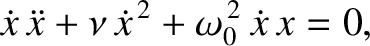 |
(2.19) |
which can be rearranged to give
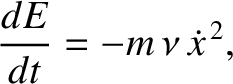 |
(2.20) |
where
 |
(2.21) |
is the total energy of the system; that is, the sum of the kinetic and potential energies. Because the right-hand side of (2.20)
cannot be positive, and is only zero when the system is stationary, the
total energy is not a conserved quantity, but instead decays monotonically in time due to the action of the damping. The net rate at which the force (2.1) does work
on the mass is
 |
(2.22) |
The spring force (i.e., the first term on the right-hand side) does negative work
on the mass (i.e., it reduces the system kinetic energy) when 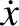 and
and  are of the same sign, and does positive work when they are of the opposite sign. It can easily be demonstrated that, on average,
the spring force does no net work on the mass during an oscillation cycle. The
damping force, on the other hand, (i.e., the second term on the right-hand side)
always does negative work on the mass, and, therefore, always acts to reduce the
system kinetic energy.
are of the same sign, and does positive work when they are of the opposite sign. It can easily be demonstrated that, on average,
the spring force does no net work on the mass during an oscillation cycle. The
damping force, on the other hand, (i.e., the second term on the right-hand side)
always does negative work on the mass, and, therefore, always acts to reduce the
system kinetic energy.
 takes the form
where
takes the form
where 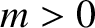 is the mass,
is the mass, 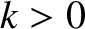 the spring force constant, and
the spring force constant, and  a constant (with the dimensions of angular frequency) that parameterizes the strength of the damping. The time evolution equation of the
system thus becomes [cf., Equation (1.2)]
where
a constant (with the dimensions of angular frequency) that parameterizes the strength of the damping. The time evolution equation of the
system thus becomes [cf., Equation (1.2)]
where
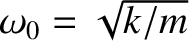 is the undamped oscillation frequency [cf., Equation (1.6)]. We shall
refer to the preceding equation as the damped harmonic oscillator equation.
is the undamped oscillation frequency [cf., Equation (1.6)]. We shall
refer to the preceding equation as the damped harmonic oscillator equation.
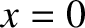 . Suppose that
. Suppose that 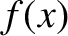 is the restoring force. It follows that
is the restoring force. It follows that
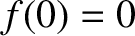 and
and
 , otherwise
, otherwise 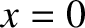 is not a stable equilibrium point. Taylor expanding about
is not a stable equilibrium point. Taylor expanding about 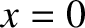 (Riley 1974), we obtain
(Riley 1974), we obtain
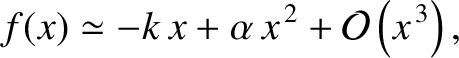
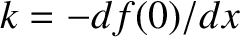 , and
, and
 . It follows that, provided the magnitude of the displacement from the
equilibrium point,
. It follows that, provided the magnitude of the displacement from the
equilibrium point, 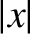 , remains sufficiently small, we can always approximate
, remains sufficiently small, we can always approximate 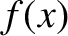 by the first non-zero term in its Taylor
expansion; that is,
by the first non-zero term in its Taylor
expansion; that is,
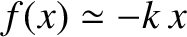 . Thus, the first term that appears on the right-hand side of Equation (2.1)
is exact (as long as the amplitude of the motion remains sufficiently small). The second term, on the other hand,
which represents the damping force, is completely phenomenological. In other words, damping forces that
arise in nature are not necessarily directly proportional to the instantaneous velocity of the system. For example,
the damping force that arises from air resistance is usually directly proportional to the square of the
instantaneous velocity (Batchelor 2000). In fact, the only reason that we have chosen a damping force that is
directly proportional to the instantaneous velocity is that it leads to a linear equation of motion.
. Thus, the first term that appears on the right-hand side of Equation (2.1)
is exact (as long as the amplitude of the motion remains sufficiently small). The second term, on the other hand,
which represents the damping force, is completely phenomenological. In other words, damping forces that
arise in nature are not necessarily directly proportional to the instantaneous velocity of the system. For example,
the damping force that arises from air resistance is usually directly proportional to the square of the
instantaneous velocity (Batchelor 2000). In fact, the only reason that we have chosen a damping force that is
directly proportional to the instantaneous velocity is that it leads to a linear equation of motion.
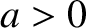 ,
, 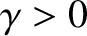 ,
,
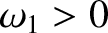 , and
, and  are all constants. By analogy
with the discussion in Section 1.2, we can interpret the
preceding solution as a periodic oscillation, of fixed angular frequency
are all constants. By analogy
with the discussion in Section 1.2, we can interpret the
preceding solution as a periodic oscillation, of fixed angular frequency 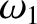 ,
and phase angle
,
and phase angle  , whose amplitude decays exponentially in
time as
, whose amplitude decays exponentially in
time as
 . It can be demonstrated that
. It can be demonstrated that

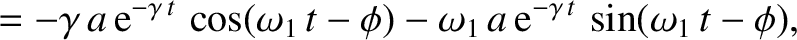
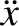
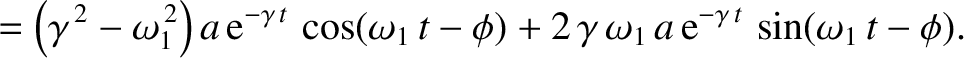
![$\displaystyle =\left[ \left(\gamma^{\,2}-\omega_1^{\,2}\right) -\nu\,\gamma + \omega_0^{\,2}\right]a\,{\rm e}^{-\gamma\,t}\,\cos(\omega_1\,t-\phi)$](img432.png)
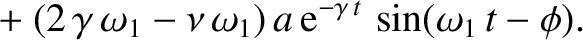
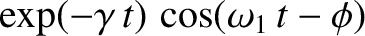 and
and
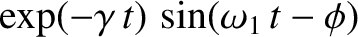 separately equate to zero, so that
separately equate to zero, so that
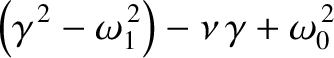
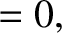

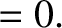
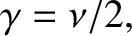
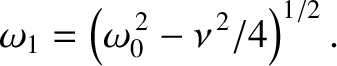
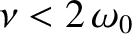 (because
(because
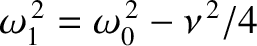 cannot be negative). We conclude that the effect of a relatively small amount of damping, parameterized
by the damping constant,
cannot be negative). We conclude that the effect of a relatively small amount of damping, parameterized
by the damping constant, 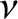 ,
on a system that exhibits simple harmonic oscillation about a stable equilibrium state is to reduce the
angular frequency of the oscillation from its undamped value
,
on a system that exhibits simple harmonic oscillation about a stable equilibrium state is to reduce the
angular frequency of the oscillation from its undamped value 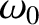 to
to
 , and to cause the amplitude of the oscillation to decay exponentially
in time at the rate
, and to cause the amplitude of the oscillation to decay exponentially
in time at the rate 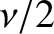 . This modified type of oscillation, which we shall refer to as damped harmonic oscillation, is illustrated in Figure 2.1.
Incidentally, if the damping is sufficiently large that
. This modified type of oscillation, which we shall refer to as damped harmonic oscillation, is illustrated in Figure 2.1.
Incidentally, if the damping is sufficiently large that
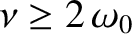 (which we shall assume not to be the case) then
the system does not oscillate at all, and any motion simply decays away exponentially
in time. (See Exercise 7.)
(which we shall assume not to be the case) then
the system does not oscillate at all, and any motion simply decays away exponentially
in time. (See Exercise 7.)
![\includegraphics[width=0.8\textwidth]{Chapter02/fig2_01.eps}](img450.png)
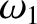 , and decay rate,
, and decay rate, 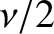 ,
of the damped harmonic oscillation specified in Equation (2.12) are determined by the constants appearing in the damped harmonic oscillator equation, (2.2), the initial amplitude,
,
of the damped harmonic oscillation specified in Equation (2.12) are determined by the constants appearing in the damped harmonic oscillator equation, (2.2), the initial amplitude,  , and the phase angle,
, and the phase angle,  ,
of the oscillation
are determined by the initial conditions. In fact, if
,
of the oscillation
are determined by the initial conditions. In fact, if 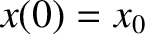 and
and
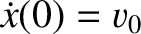 then it follows from Equation (2.12) that
then it follows from Equation (2.12) that

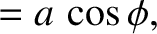
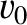
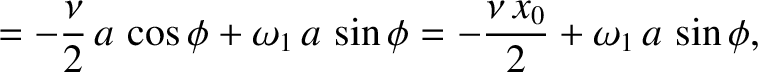
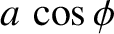
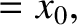
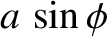
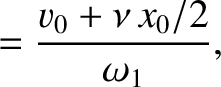
![$\displaystyle =\left[x_0^{\,2} + \left(\frac{v_0+\nu\,x_0/2}{\omega_1}\right)^2\right]^{1/2},$](img462.png)
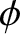
 is a
solution then so is
is a
solution then so is 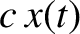 , where
, where 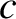 is an arbitrary constant. It follows
that the solutions of this equation are superposable,
so that if
is an arbitrary constant. It follows
that the solutions of this equation are superposable,
so that if 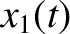 and
and 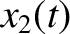 are two solutions corresponding to different initial
conditions then
are two solutions corresponding to different initial
conditions then
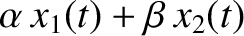 is a third solution, where
is a third solution, where 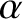 and
and 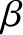 are arbitrary constants.
are arbitrary constants.
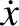 ,
we obtain
,
we obtain
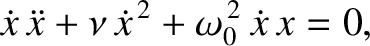


 and
and  are of the same sign, and does positive work when they are of the opposite sign. It can easily be demonstrated that, on average,
the spring force does no net work on the mass during an oscillation cycle. The
damping force, on the other hand, (i.e., the second term on the right-hand side)
always does negative work on the mass, and, therefore, always acts to reduce the
system kinetic energy.
are of the same sign, and does positive work when they are of the opposite sign. It can easily be demonstrated that, on average,
the spring force does no net work on the mass during an oscillation cycle. The
damping force, on the other hand, (i.e., the second term on the right-hand side)
always does negative work on the mass, and, therefore, always acts to reduce the
system kinetic energy.