


Next: Volume Integrals
Up: Vectors
Previous: Line Integrals
Surface integrals often arise in Physics. For instance, the rate of
flow of a liquid of velocity 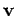 through an infinitesimal
surface of vector area
through an infinitesimal
surface of vector area 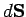 is
is
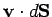 (i.e., the product of the normal component of the velocity,
(i.e., the product of the normal component of the velocity,  , and the magnitude of the area,
, and the magnitude of the area, 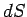 , where
, where 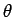 is the angle subtended between
is the angle subtended between 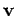 and
and 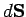 ). The net rate of flow through a surface
). The net rate of flow through a surface 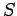 made up
of
very many infinitesimal surfaces is
made up
of
very many infinitesimal surfaces is
![\begin{displaymath}
\int_{S} {\bf v}\cdot d{\bf S} = \lim_{d{\bf S}\rightarrow 0}\left[ \sum v\,\cos\theta
\,dS\right],
\end{displaymath}](img203.png) |
(48) |
where 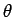 is the angle subtended between a surface element
is the angle subtended between a surface element 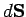 and the local
flow velocity
and the local
flow velocity
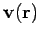 . If the surface is closed, and the surface elements all point outward, then the integral is conventionally written
. If the surface is closed, and the surface elements all point outward, then the integral is conventionally written
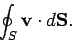 |
(49) |
In this case, the integral is often termed the flux of the velocity field
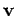 out of the closed surface
out of the closed surface 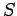 .
.
Richard Fitzpatrick
2007-07-14