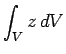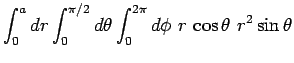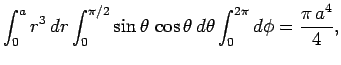Volume Integrals

Next: Electricity Up: Vectors Previous: Surface Integrals

Volume Integrals

A volume integral takes the form

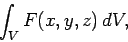$\begin{displaymath} \int_V F(x,y,z)\,dV, \end{displaymath}$

(50)

where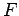

is a three-dimensional mathematical function,

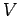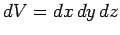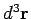some volume in space, and $dV = dx \,dy \,dz$ an element of this volume. The volume element is sometimes written $d^3{\bf r}$ .

As an example of a volume integral, let us evaluate the centre of gravity of a solid hemisphere of radius 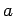(centered on the origin). The height of the centre of gravity is given by

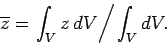$\begin{displaymath} \overline{z} = \left. \int_V z\,dV\right/ \int_V dV. \end{displaymath}$

(51)

The bottom integral is simply the volume of the hemisphere, which is 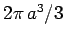$2\pi \,a^3/3$ . The top integral is most easily evaluated in spherical polar coordinates (

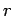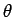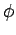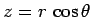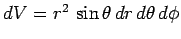, $\theta$ , $\phi$ ), for which $z= r\,\cos\theta$ and $dV = r^2\,\sin\theta\,dr\,d\theta\,d\phi$ . Thus,

$\displaystyle \int_V z\,dV$	$\textstyle =$	$\displaystyle \int_0^a dr\int_0^{\pi/2} d\theta \int_0^{2\pi} d\phi\,\,r\,\cos\theta\, \, r^2 \sin\theta$
	$\textstyle =$	$\displaystyle \int_0^a r^3\,dr \int_0^{\pi/2} \sin\theta \,\cos\theta\,d\theta \int_0^{2\pi} d\phi = \frac{\pi \,a^4}{4},$	(52)

giving

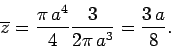$\begin{displaymath} \overline{z} = \frac{ \pi \,a^4}{4}\frac{3}{2\pi \,a^3}= \frac{3\,a}{8}. \end{displaymath}$

(53)

Next: Electricity Up: Vectors Previous: Surface Integrals

Richard Fitzpatrick 2007-07-14