Motion on curved surfaces

Consider a smooth rigid vertical hoop of internal radius $r$, as shown in Fig. 65. Suppose that an object of mass $m$ slides without friction around the inside of this hoop. What is the motion of this object? Is it possible for the object to execute a complete vertical circle?

Figure 65: Motion on the inside of a vertical hoop.

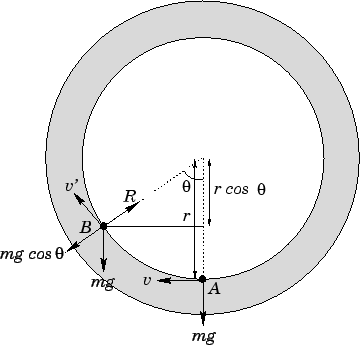
Suppose that the object moves from point $A$ to point $B$ in Fig. 65. In doing so, it gains potential energy $m g r (1-\cos\theta)$, where $\theta$ is the angular coordinate of the object measured with respect to the downward vertical. This gain in potential energy must be offset by a corresponding loss in kinetic energy. Thus,

$$\frac{1}{2} m v^2 - \frac{1}{2} m {v'}^2 = m g r (1-\cos\theta),$$ (298)

which reduces to

$${v'}^2 = v^2 - 2 r g (1-\cos\theta).$$ (299)

Here, $v$ is the velocity at point $A$ ( $\theta=0^\circ$), and $v'$ is the velocity at point $B$ ( $\theta =\theta^\circ$).

Let us now examine the radial acceleration of the object at point $B$. The radial forces acting on the object are the reaction $R$ of the vertical hoop, which acts towards the centre of the hoop, and the component $m g \cos\theta$ of the object's weight, which acts away from the centre of the hoop. Since the object is executing circular motion with instantaneous tangential velocity $v'$, it must experience an instantaneous acceleration ${v'}^2/r$ towards the centre of the hoop. Hence, Newton's second law of motion yields

$$\frac{m {v'}^2}{r} = R - m g \cos\theta.$$ (300)

Note, however, that there is a constraint on the reaction $R$ that the hoop can exert on the object. This reaction must always be positive. In other words, the hoop can push the object away from itself, but it can never pull it towards itself. Another way of putting this is that if the reaction ever becomes negative then the object will fly off the surface of the hoop, since it is no longer being pressed into this surface. It should be clear, by now, that the problem we are considering is exactly analogous to the earlier problem of an object attached to the end of a piece of string which is executing a vertical circle, with the reaction $R$ of the hoop playing the role of the tension $T$ in the string.

Let us imagine that the hoop under consideration is a ``loop the loop'' segment in a fairground roller-coaster. The object sliding around the inside of the loop then becomes the roller-coaster train. Suppose that the fairground operator can vary the velocity $v$ with which the train is sent into the bottom of the loop (i.e., the velocity at $\theta=0^\circ$). What is the safe range of $v$? Now, if the train starts at $\theta=0^\circ$ with velocity $v$ then there are only three possible outcomes. Firstly, the train can execute a complete circuit of the loop. Secondly, the train can slide part way up the loop, come to a halt, reverse direction, and then slide back down again. Thirdly, the train can slide part way up the loop, but then fall off the loop. Obviously, it is the third possibility that the fairground operator would wish to guard against.

Using the analogy between this problem and the problem of a mass on the end of a piece of string executing a vertical circle, the condition for the roller-coaster train to execute a complete circuit is

$$v^2 > 5 r g.$$ (301)

Note, interestingly enough, that this condition is independent of the mass of the train.

Equation (300) yields

$${v'}^2 = \frac{r R}{m} - r g \cos\theta.$$ (302)

Now, the condition for the train to reverse direction without falling off the loop is ${v'}^2=0$ with $R>0$. Thus, the train reverses direction when

$$R = m g \cos\theta.$$ (303)

Note that this equation can only be satisfied for positive $R$ when $\cos\theta>0$. In other words, the train can only turn around without falling off the loop if the turning point lies in the lower half of the loop (i.e., $-90^\circ<\theta<90^\circ$). The condition for the train to fall off the loop is

$${v'}^2 =- r g \cos\theta.$$ (304)

Note that this equation can only be satisfied for positive ${v'}^2$ when $\cos\theta<0$. In other words, the train can only fall off the loop when it is situated in the upper half of the loop. It is fairly clear that if the train's initial velocity is not sufficiently large for it to execute a complete circuit of the loop, and not sufficiently small for it to turn around before entering the upper half of the loop, then it must inevitably fall off the loop somewhere in the loop's upper half. The critical value of $v^2$ above which the train executes a complete circuit is $5 r g$ [see Eq. (301)]. The critical value of $v^2$ at which the train just turns around before entering the upper half of the loop is $2 r g$ [this is obtained from Eq. (299) by setting $v'=0$ and $\theta =90^\circ$]. Hence, the dangerous range of $v^2$ is

$$2 r g < v^2< 5 r g.$$ (305)

For $v^2<2 r g$, the train turns around in the lower half of the loop. For $v^2 > 5 r g$, the train executes a complete circuit around the loop. However, for $2 r g < v^2< 5 r g$, the train falls off the loop somewhere in its upper half.

Figure 66: A skier on a hemispherical mountain.

Consider a skier of mass $m$ skiing down a hemispherical mountain of radius $r$, as shown in Fig. 66. Let $\theta$ be the angular coordinate of the skier, measured with respect to the upward vertical. Suppose that the skier starts at rest ($v=0$) on top of the mountain ( $\theta=0^\circ$), and slides down the mountain without friction. At what point does the skier fly off the surface of the mountain?

Suppose that the skier has reached angular coordinate $\theta$. At this stage, the skier has fallen though a height $r (1-\cos\theta)$. Thus, the tangential velocity $v$ of the skier is given by energy conservation:

$$\frac{1}{2} m v^2 = m g r (1-\cos\theta).$$ (306)

Let us now consider the skier's radial acceleration. The radial forces acting on the skier are the reaction $R$ exerted by the mountain, which acts radially outwards, and the component of the skier's weight $m g \cos\theta$, which acts radially inwards. Since the skier is executing circular motion, radius $r$, with instantaneous tangential velocity $v$, he/she experiences an instantaneous inward radial acceleration $v^2/r$. Hence, Newton's second law of motion yields

$$m \frac{v^2}{r} = m g \cos\theta - R.$$ (307)

Equations (306) and (307) can be combined to give

$$R = m g (3 \cos\theta-2).$$ (308)

As before, the reaction $R$ is constrained to be positive--the mountain can push outward on the skier, but it cannot pull the skier inward. In fact, as soon as the reaction becomes negative, the skier flies of the surface of the mountain. This occurs when $\cos\theta_0 = 2/3$, or $\theta_0 = 48.19^\circ$. The height through which the skier falls before becoming a ski-jumper is $h=r (1-\cos\theta_0) = a/3$.