The vertical pendulum

Let us now examine an example of non-uniform circular motion. Suppose that an object of mass $m$ is attached to the end of a light rigid rod, or light string, of length $r$. The other end of the rod, or string, is attached to a stationary pivot in such a manner that the object is free to execute a vertical circle about this pivot. Let $\theta$ measure the angular position of the object, measured with respect to the downward vertical. Let $v$ be the velocity of the object at $\theta=0^\circ$. How large do we have to make $v$ in order for the object to execute a complete vertical circle?

Figure 64: Motion in a vertical circle.

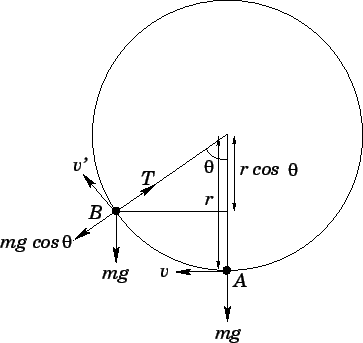
Consider Fig. 64. Suppose that the object moves from point $A$, where its tangential velocity is $v$, to point $B$, where its tangential velocity is $v'$. Let us, first of all, obtain the relationship between $v$ and $v'$. This is most easily achieved by considering energy conservation. At point $A$, the object is situated a vertical distance $r$ below the pivot, whereas at point $B$ the vertical distance below the pivot has been reduced to $r \cos\theta$. Hence, in moving from $A$ to $B$ the object gains potential energy $m g r (1-\cos\theta)$. This gain in potential energy must be offset by a corresponding loss in kinetic energy. Thus,

$$\frac{1}{2} m v^2 - \frac{1}{2} m {v'}^2 = m g r (1-\cos\theta),$$ (290)

which reduces to

$${v'}^2 = v^2 - 2 r g (1-\cos\theta).$$ (291)

Let us now examine the radial acceleration of the object at point $B$. The radial forces acting on the object are the tension $T$ in the rod, or string, which acts towards the centre of the circle, and the component $m g \cos\theta$ of the object's weight, which acts away from the centre of the circle. Since the object is executing circular motion with instantaneous tangential velocity $v'$, it must experience an instantaneous acceleration ${v'}^2/r$ towards the centre of the circle. Hence, Newton's second law of motion yields

$$\frac{m {v'}^2}{r} = T - m g \cos\theta.$$ (292)

Equations (291) and (292) can be combined to give

$$T = \frac{m v^2}{r} + m g (3 \cos\theta -2).$$ (293)

Suppose that the object is, in fact, attached to the end of a piece of string, rather than a rigid rod. One important property of strings is that, unlike rigid rods, they cannot support negative tensions. In other words, a string can only pull objects attached to its two ends together--it cannot push them apart. Another way of putting this is that if the tension in a string ever becomes negative then the string will become slack and collapse. Clearly, if our object is to execute a full vertical circle then then tension $T$ in the string must remain positive for all values of $\theta$. It is clear from Eq. (293) that the tension attains its minimum value when $\theta =180^\circ$ (at which point $\cos\theta=-1$). This is hardly surprising, since $\theta =180^\circ$ corresponds to the point at which the object attains its maximum height, and, therefore, its minimum tangential velocity. It is certainly the case that if the string tension is positive at this point then it must be positive at all other points. Now, the tension at $\theta =180^\circ$ is given by

$$T_0 = \frac{m v^2}{r} -5 m g.$$ (294)

Hence, the condition for the object to execute a complete vertical circle without the string becoming slack is $T_0>0$, or

$$v^2 > 5 r g.$$ (295)

Note that this condition is independent of the mass of the object.

Suppose that the object is attached to the end of a rigid rod, instead of a piece of string. There is now no constraint on the tension, since a rigid rod can quite easily support a negative tension (i.e., it can push, as well as pull, on objects attached to its two ends). However, in order for the object to execute a complete vertical circle the square of its tangential velocity ${v'}^2$ must remain positive at all values of $\theta$. It is clear from Eq. (291) that ${v'}^2$ attains its minimum value when $\theta =180^\circ$. This is, again, hardly surprising. Thus, if ${v'}^2$ is positive at this point then it must be positive at all other points. Now, the expression for ${v'}^2$ at $\theta =180^\circ$ is

$$({v'}^2)_0 = v^2 - 4 r g.$$ (296)

Hence, the condition for the object to execute a complete vertical circle is $({v'}^2)_0 >0$, or

$$v^2 > 4 r g.$$ (297)

Note that this condition is slightly easier to satisfy than the condition (295). In other words, it is slightly easier to cause an object attached to the end of a rigid rod to execute a vertical circle than it is to cause an object attached to the end of a string to execute the same circle. The reason for this is that the rigidity of the rod helps support the object when it is situated above the pivot point.