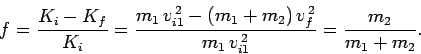Next: Collisions in 2-dimensions
Up: Conservation of momentum
Previous: Impulses
Figure 54:
A collision in 1-dimension.
 |
Consider two objects of mass 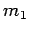 and
and 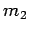 , respectively, which are free
to move in 1-dimension. Suppose that these two objects collide.
Suppose, further, that both objects are subject to zero net force when they are
not in contact with one another. This situation is illustrated in Fig. 54.
, respectively, which are free
to move in 1-dimension. Suppose that these two objects collide.
Suppose, further, that both objects are subject to zero net force when they are
not in contact with one another. This situation is illustrated in Fig. 54.
Both before and after the collision, the two objects move with constant velocity.
Let  and
and  be the velocities of the first and second objects, respectively,
before the collision. Likewise, let
be the velocities of the first and second objects, respectively,
before the collision. Likewise, let 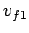 and
and 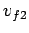 be the velocities of
the first and second objects, respectively,
after the collision. During the collision itself, the first object exerts a large
transitory force
be the velocities of
the first and second objects, respectively,
after the collision. During the collision itself, the first object exerts a large
transitory force 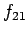 on the second, whereas the second object exerts an
equal and opposite force
on the second, whereas the second object exerts an
equal and opposite force
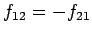 on the first. In fact, we can model the collision
as equal and opposite impulses given to the two objects at the instant in time
when they come together.
on the first. In fact, we can model the collision
as equal and opposite impulses given to the two objects at the instant in time
when they come together.
We are clearly considering a system in which there is zero net external force (the forces
associated with the collision are internal in nature). Hence, the total momentum of the
system is a conserved quantity. Equating the total momenta before and after the
collision, we obtain
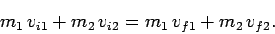 |
(217) |
This equation is valid for any 1-dimensional
collision, irrespective its nature. Note that, assuming
we know the masses of the colliding objects, the above equation only fully describes the
collision if we are given the initial velocities of both objects, and the final velocity of
at least one of the objects. (Alternatively, we could be given both final velocities and only
one of the initial velocities.)
There are many different types of collision. An elastic collision is one in which
the total kinetic energy of the two colliding objects is the same
before and after the collision. Thus, for an elastic collision we can write
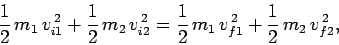 |
(218) |
in addition to Eq. (217). Hence, in this case, the collision is fully specified
once we are given the two initial velocities of the colliding objects. (Alternatively,
we could be given the two final velocities.)
The majority of collisions occurring in real life are not elastic in nature.
Some fraction of the initial kinetic
energy of the colliding objects is usually converted into some other form of energy--generally
heat energy, or energy associated with the mechanical deformation of the objects--during the
collision. Such collisions are termed inelastic. For instance, a large fraction of
the initial kinetic energy of a typical automobile accident is converted into mechanical
energy of deformation of the two vehicles. Inelastic collisions also occur during squash/racquetball/handball
games: in each case, the ball becomes warm to the touch after a long game, because some
fraction of the
ball's kinetic energy of collision with the walls of the court has been converted into
heat energy. Equation (217) remains valid for inelastic collisions--however, Eq. (218)
is invalid. Thus, generally speaking, an inelastic collision is only fully characterized
when we are given the initial velocities of both objects, and the final velocity of
at least one of the objects.
There is, however,
a special case of an inelastic collision--called a totally inelastic collision--which
is fully characterized once we are given the initial velocities of the colliding objects.
In a totally inelastic collision, the two objects stick together after the collision, so
that 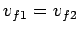 .
.
Let us, now, consider elastic collisions in more detail. Suppose that we transform to a frame of
reference which co-moves with the centre of mass of the system. The motion of a multi-component system
often looks particularly simple when viewed
in such a frame. Since the system is subject to zero net external force, the velocity of the
centre of mass is invariant, and is given by
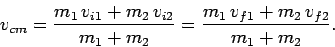 |
(219) |
An object which possesses a velocity  in our original frame of reference--henceforth, termed
the laboratory frame--possesses a velocity
in our original frame of reference--henceforth, termed
the laboratory frame--possesses a velocity 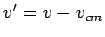 in the centre of mass
frame. It is easily demonstrated that
in the centre of mass
frame. It is easily demonstrated that
The above equations yield
 |
|
|
(224) |
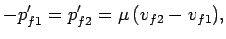 |
|
|
(225) |
where
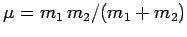 is the
so-called reduced mass, and
is the
so-called reduced mass, and
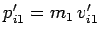 is the initial momentum of the first object in the
centre of mass frame, etc. In other words, when viewed in the centre of mass frame, the
two objects approach one another with equal and opposite momenta before the collision,
and diverge from one another with equal and opposite momenta after the collision.
Thus, the centre of mass momentum conservation equation,
is the initial momentum of the first object in the
centre of mass frame, etc. In other words, when viewed in the centre of mass frame, the
two objects approach one another with equal and opposite momenta before the collision,
and diverge from one another with equal and opposite momenta after the collision.
Thus, the centre of mass momentum conservation equation,
 |
(226) |
is trivially satisfied, because both the left- and right-hand sides are zero. Incidentally,
this result is valid for both elastic and inelastic collisions.
The centre of mass kinetic energy conservation equation takes the form
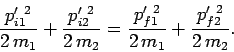 |
(227) |
Note, incidentally, that if energy and momentum are conserved in the laboratory frame then
they must also be conserved in the centre of mass frame. A comparison
of Eqs. (224), (225), and (227) yields
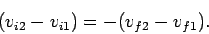 |
(228) |
In other words, the relative velocities of the colliding objects are equal and
opposite before and after the collision. This is true in all frames of
reference, since relative velocities are frame invariant. Note, however, that this
result only applies to fully elastic collisions.
Equations (217) and (228) can be combined to give the following
pair of equations which fully specify the final velocities (in the laboratory frame) of two objects
which collide elastically, given their initial velocities:
Let us, now, consider some special cases. Suppose that two equal mass objects collide elastically.
If 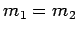 then Eqs. (229) and (230) yield
then Eqs. (229) and (230) yield
 |
|
|
(231) |
 |
|
|
(232) |
In other words, the two objects simply exchange velocities when they collide.
For instance, if the second object is stationary and the first object strikes it head-on
with velocity  then the first object is brought to a halt whereas the second object
moves off with velocity
then the first object is brought to a halt whereas the second object
moves off with velocity  . It is possible to reproduce this effect in pool
by striking the cue ball with great force in such a manner that it slides, rather
that rolls, over the table--in this case, when the cue ball strikes another ball head-on
it comes to a complete halt, and the other ball is propelled forward very rapidly.
Incidentally, it is necessary to prevent the cue ball from rolling, because rolling motion
is not taken into account in our analysis, and actually changes the answer.
. It is possible to reproduce this effect in pool
by striking the cue ball with great force in such a manner that it slides, rather
that rolls, over the table--in this case, when the cue ball strikes another ball head-on
it comes to a complete halt, and the other ball is propelled forward very rapidly.
Incidentally, it is necessary to prevent the cue ball from rolling, because rolling motion
is not taken into account in our analysis, and actually changes the answer.
Suppose that the second object is much more massive than the first (i.e., 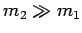 )
and is initially at rest (i.e.,
)
and is initially at rest (i.e., 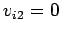 ). In this case, Eqs. (229) and (230) yield
). In this case, Eqs. (229) and (230) yield
In other words, the velocity of the light object is effectively reversed during the collision, whereas
the massive object remains approximately at rest. Indeed, this is the sort of behaviour we
expect when an object collides elastically with an immovable obstacle: e.g., when an
elastic ball bounces off a brick wall.
Suppose, finally, that the second object is much lighter than the first (i.e., 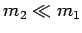 )
and is initially at rest (i.e.,
)
and is initially at rest (i.e., 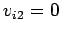 ). In this case, Eqs. (229) and (230) yield
). In this case, Eqs. (229) and (230) yield
In other words, the motion of the massive object is essentially unaffected by the collision,
whereas the light object ends up going twice as fast as the massive one.
Let us, now, consider totally inelastic collisions in more detail. In a totally inelastic
collision the two objects stick together after colliding, so they
end up moving with the same final velocity
 . In this case, Eq. (217) reduces to
. In this case, Eq. (217) reduces to
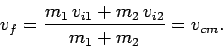 |
(237) |
In other words, the common final velocity of the two objects is equal to the
centre of mass velocity of the system. This is hardly a surprising result. We have already seen
that in the centre of mass frame the two objects must diverge with equal and opposite momenta after
the collision. However, in a totally inelastic collision these two momenta must
also be equal (since the two objects stick together). The only way in which this is possible
is if the two objects remain stationary in the centre of mass frame after the collision.
Hence, the two objects move with the centre of mass velocity in the laboratory frame.
Suppose that the second object is initially at rest (i.e., 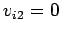 ). In this
special case, the common final velocity of the two objects is
). In this
special case, the common final velocity of the two objects is
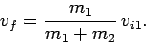 |
(238) |
Note that the first object is slowed down by the collision.
The fractional loss in kinetic energy of the system due to the collision is given
by
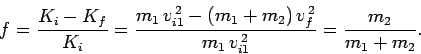 |
(239) |
The loss in kinetic energy is small if the (initially) stationary object
is much lighter than the moving object (i.e., if 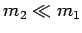 ), and almost
), and almost 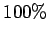 if the moving
object is much lighter than the stationary one (i.e., if
if the moving
object is much lighter than the stationary one (i.e., if 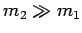 ).
Of course, the lost kinetic energy of the
system is converted into some other form of energy: e.g., heat energy.
).
Of course, the lost kinetic energy of the
system is converted into some other form of energy: e.g., heat energy.
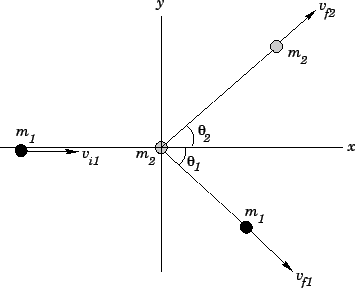
Figure 55:
A collision in 2-dimensions.
 |



Next: Collisions in 2-dimensions
Up: Conservation of momentum
Previous: Impulses
Richard Fitzpatrick
2006-02-02

![]() and
and ![]() be the velocities of the first and second objects, respectively,
before the collision. Likewise, let
be the velocities of the first and second objects, respectively,
before the collision. Likewise, let ![]() and
and ![]() be the velocities of
the first and second objects, respectively,
after the collision. During the collision itself, the first object exerts a large
transitory force
be the velocities of
the first and second objects, respectively,
after the collision. During the collision itself, the first object exerts a large
transitory force ![]() on the second, whereas the second object exerts an
equal and opposite force
on the second, whereas the second object exerts an
equal and opposite force
![]() on the first. In fact, we can model the collision
as equal and opposite impulses given to the two objects at the instant in time
when they come together.
on the first. In fact, we can model the collision
as equal and opposite impulses given to the two objects at the instant in time
when they come together.
![]() .
.
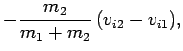
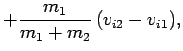
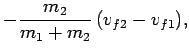
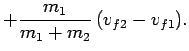
![]() then Eqs. (229) and (230) yield
then Eqs. (229) and (230) yield
![]() )
and is initially at rest (i.e.,
)
and is initially at rest (i.e., ![]() ). In this case, Eqs. (229) and (230) yield
). In this case, Eqs. (229) and (230) yield
![]() )
and is initially at rest (i.e.,
)
and is initially at rest (i.e., ![]() ). In this case, Eqs. (229) and (230) yield
). In this case, Eqs. (229) and (230) yield
![]() . In this case, Eq. (217) reduces to
. In this case, Eq. (217) reduces to
![]() ). In this
special case, the common final velocity of the two objects is
). In this
special case, the common final velocity of the two objects is