


Next: Collisions in 1-dimension
Up: Conservation of momentum
Previous: Rocket science
Impulses
Figure 52:
A ball bouncing off a wall.
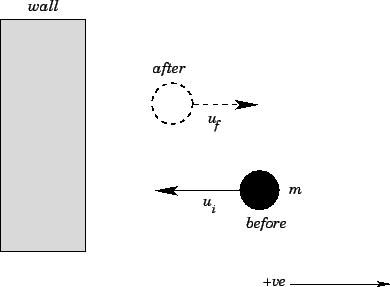 |
Suppose that a ball of mass  and speed
and speed 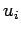 strikes an immovable wall normally and
rebounds with speed
strikes an immovable wall normally and
rebounds with speed 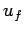 . See Fig. 52. Clearly, the momentum of the ball is changed
by the collision with the wall, since the direction of the ball's velocity is reversed.
It follows that the wall must exert a force on the ball, since force is the rate of change
of momentum. This force is generally very large, but is only exerted for the short instance in time
during which the ball is in physical contact with the wall. As we have already mentioned, physicists
generally refer to such a force as an impulsive force.
. See Fig. 52. Clearly, the momentum of the ball is changed
by the collision with the wall, since the direction of the ball's velocity is reversed.
It follows that the wall must exert a force on the ball, since force is the rate of change
of momentum. This force is generally very large, but is only exerted for the short instance in time
during which the ball is in physical contact with the wall. As we have already mentioned, physicists
generally refer to such a force as an impulsive force.
Figure 53:
An impulsive force.
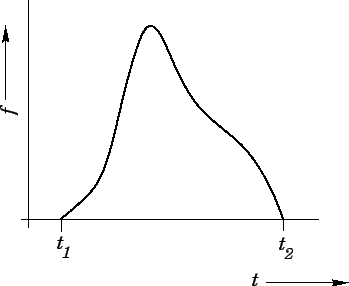 |
Figure 53 shows the typical time history of an impulsive force,  . It can be seen that
the force is only non-zero in the short time interval
. It can be seen that
the force is only non-zero in the short time interval 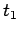 to
to 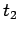 . It is helpful
to define a quantity known as the net impulse,
. It is helpful
to define a quantity known as the net impulse, 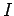 , associated with
, associated with  :
:
 |
(210) |
In other words, 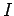 is the total area under the
is the total area under the  curve shown in Fig. 53.
curve shown in Fig. 53.
Consider a object subject to the impulsive force pictured in Fig. 53. Newton's
second law of motion yields
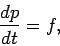 |
(211) |
where  is the momentum of the object. Integrating the above equation, making use of
the definition (210), we obtain
is the momentum of the object. Integrating the above equation, making use of
the definition (210), we obtain
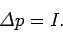 |
(212) |
Here,
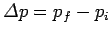 , where
, where  is the momentum before the impulse, and
is the momentum before the impulse, and
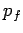 is the momentum after the impulse. We conclude that the net change in momentum of
an object subject to an impulsive force is equal to the total impulse associated with that
force. For instance, the net change in momentum of the ball bouncing off the wall in
Fig. 52 is
is the momentum after the impulse. We conclude that the net change in momentum of
an object subject to an impulsive force is equal to the total impulse associated with that
force. For instance, the net change in momentum of the ball bouncing off the wall in
Fig. 52 is
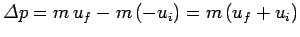 . [Note: The initial velocity is
. [Note: The initial velocity is 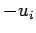 , since the ball is initially
moving in the negative direction.]
It follows that the net impulse imparted
to the ball by the wall is
, since the ball is initially
moving in the negative direction.]
It follows that the net impulse imparted
to the ball by the wall is
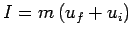 . Suppose that we know the ball was only in physical
contact with the wall for the short time interval
. Suppose that we know the ball was only in physical
contact with the wall for the short time interval
 . We conclude that the
average force
. We conclude that the
average force  exerted on the ball during this time interval
was
exerted on the ball during this time interval
was
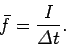 |
(213) |
The above discussion is only relevant to 1-dimensional motion. However, the generalization
to 3-dimensional motion is fairly straightforward. Consider an impulsive force
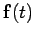 , which is only non-zero in the short time interval
, which is only non-zero in the short time interval 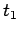 to
to 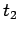 .
The vector impulse associated with this force is simply
.
The vector impulse associated with this force is simply
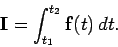 |
(214) |
The net change in momentum of an object subject to 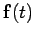 is
is
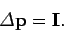 |
(215) |
Finally, if
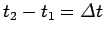 , then the average force experienced by the
object in the time interval
, then the average force experienced by the
object in the time interval 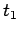 to
to 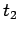 is
is
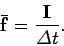 |
(216) |



Next: Collisions in 1-dimension
Up: Conservation of momentum
Previous: Rocket science
Richard Fitzpatrick
2006-02-02

![]() . It can be seen that
the force is only non-zero in the short time interval
. It can be seen that
the force is only non-zero in the short time interval ![]() to
to ![]() . It is helpful
to define a quantity known as the net impulse,
. It is helpful
to define a quantity known as the net impulse, ![]() , associated with
, associated with ![]() :
:
![]() , which is only non-zero in the short time interval
, which is only non-zero in the short time interval ![]() to
to ![]() .
The vector impulse associated with this force is simply
.
The vector impulse associated with this force is simply