 |
Let us apply Newton's second law to the block. The mass of the block is ![]() , and
its acceleration is zero, since the block is assumed to be in equilibrium.
The block is subject to two forces, a downward force
, and
its acceleration is zero, since the block is assumed to be in equilibrium.
The block is subject to two forces, a downward force ![]() due to gravity, and
an upward force
due to gravity, and
an upward force ![]() due to the tension of the string. It follows that
due to the tension of the string. It follows that
| (97) |
Figure 27 shows a slightly more complicated example in which a block of mass ![]() is
suspended by three strings. The question is what are the tensions,
is
suspended by three strings. The question is what are the tensions, ![]() ,
, ![]() , and
, and ![]() , in these
strings, assuming that the block is in equilibrium? Using analogous arguments to
the previous case, we can easily demonstrate that the tension
, in these
strings, assuming that the block is in equilibrium? Using analogous arguments to
the previous case, we can easily demonstrate that the tension ![]() in the lowermost string is
in the lowermost string is
![]() . The tensions in the two uppermost strings are obtained by applying Newton's
second law of motion to the knot where all three strings meet. See Fig. 28.
. The tensions in the two uppermost strings are obtained by applying Newton's
second law of motion to the knot where all three strings meet. See Fig. 28.
There are three forces acting on the knot: the downward force ![]() due to the
tension in the lower string, and the forces
due to the
tension in the lower string, and the forces ![]() and
and ![]() due to the tensions
in the upper strings. The latter two forces act along their respective strings,
as indicate in the diagram.
Since the knot is in equilibrium, the vector sum of all the forces acting
on it must be zero.
due to the tensions
in the upper strings. The latter two forces act along their respective strings,
as indicate in the diagram.
Since the knot is in equilibrium, the vector sum of all the forces acting
on it must be zero.
Consider the horizontal components of the
forces acting on the knot. Let components acting to the right be positive, and
vice versa.
The horizontal component of tension ![]() is
zero, since this tension acts straight down. The horizontal
component of tension
is
zero, since this tension acts straight down. The horizontal
component of tension ![]() is
is
![]() , since this
force subtends an angle of
, since this
force subtends an angle of ![]() with respect to the horizontal (see Fig. 16).
Likewise, the
horizontal component of tension
with respect to the horizontal (see Fig. 16).
Likewise, the
horizontal component of tension ![]() is
is
![]() .
Since the knot does not accelerate in the horizontal direction, we can equate
the sum of these components to zero:
.
Since the knot does not accelerate in the horizontal direction, we can equate
the sum of these components to zero:
Consider the vertical components of the forces acting on the knot. Let
components acting upward be positive, and
vice versa. The vertical component of tension ![]() is
is
![]() , since this tension acts straight down. The vertical
component of tension
, since this tension acts straight down. The vertical
component of tension ![]() is
is
![]() , since this
force subtends an angle of
, since this
force subtends an angle of ![]() with respect to the horizontal (see Fig. 16).
Likewise, the
vertical component of tension
with respect to the horizontal (see Fig. 16).
Likewise, the
vertical component of tension ![]() is
is
![]() .
Since the knot does not accelerate in the vertical direction, we can equate
the sum of these components to zero:
.
Since the knot does not accelerate in the vertical direction, we can equate
the sum of these components to zero:
Finally, Eqs. (98) and (99) yield
 |
(100) | ||
| (101) |
Consider a block of mass ![]() sliding down a smooth frictionless incline
which subtends an angle
sliding down a smooth frictionless incline
which subtends an angle ![]() to the horizontal, as shown in Fig 29.
The weight
to the horizontal, as shown in Fig 29.
The weight ![]() of the block is directed vertically downwards. However,
this force can be resolved into components
of the block is directed vertically downwards. However,
this force can be resolved into components
![]() , acting
perpendicular (or normal) to the incline, and
, acting
perpendicular (or normal) to the incline, and
![]() ,
acting parallel to the incline. Note that the reaction of the incline
to the weight of the block acts normal to the incline, and only
matches the normal component of the weight: i.e., it is
of magnitude
,
acting parallel to the incline. Note that the reaction of the incline
to the weight of the block acts normal to the incline, and only
matches the normal component of the weight: i.e., it is
of magnitude
![]() . This is a general result: the reaction
of any unyielding surface is always locally
normal to that surface, directed outwards (away from the surface),
and matches the normal component of any inward force applied to the surface.
The block is clearly in equilibrium in the direction normal to
the incline, since the normal component of the block's weight is balanced by
the reaction of the incline. However, the block is subject
to the unbalanced force
. This is a general result: the reaction
of any unyielding surface is always locally
normal to that surface, directed outwards (away from the surface),
and matches the normal component of any inward force applied to the surface.
The block is clearly in equilibrium in the direction normal to
the incline, since the normal component of the block's weight is balanced by
the reaction of the incline. However, the block is subject
to the unbalanced force
![]() in the direction parallel
to the incline, and, therefore, accelerates down the slope.
Applying Newton's second law to this problem (with the coordinates shown
in the figure), we obtain
in the direction parallel
to the incline, and, therefore, accelerates down the slope.
Applying Newton's second law to this problem (with the coordinates shown
in the figure), we obtain
| (102) |
| (103) |
Consider two masses, ![]() and
and ![]() , connected by a light
inextensible string. Suppose that the first mass slides
over a smooth, frictionless, horizontal table, whilst the
second is suspended over the edge of the table by means
of a light frictionless pulley. See Fig. 30. Since the
pulley is light, we can neglect its rotational inertia in our analysis.
Moreover, no force is required to turn a frictionless pulley, so we can
assume that the tension
, connected by a light
inextensible string. Suppose that the first mass slides
over a smooth, frictionless, horizontal table, whilst the
second is suspended over the edge of the table by means
of a light frictionless pulley. See Fig. 30. Since the
pulley is light, we can neglect its rotational inertia in our analysis.
Moreover, no force is required to turn a frictionless pulley, so we can
assume that the tension
![]() of the string is the same on either side of the pulley. Let us
apply Newton's second law of motion to each mass in turn. The first mass
is subject to a downward force
of the string is the same on either side of the pulley. Let us
apply Newton's second law of motion to each mass in turn. The first mass
is subject to a downward force ![]() , due to gravity. However, this force
is completely canceled out by the upward reaction force due to the table.
The mass
, due to gravity. However, this force
is completely canceled out by the upward reaction force due to the table.
The mass ![]() is also subject to a horizontal force
is also subject to a horizontal force ![]() , due to
the tension in the string, which causes it to move rightwards
with acceleration
, due to
the tension in the string, which causes it to move rightwards
with acceleration
| (104) |
| (105) |
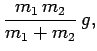 |
(106) | ||
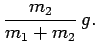 |
(107) |
Consider two masses, ![]() and
and ![]() , connected by a light
inextensible string which is suspended from a light frictionless
pulley, as shown in Fig. 31. Let us again apply Newton's
second law to each mass in turn. Without being given the values
of
, connected by a light
inextensible string which is suspended from a light frictionless
pulley, as shown in Fig. 31. Let us again apply Newton's
second law to each mass in turn. Without being given the values
of ![]() and
and ![]() , we cannot determine beforehand which mass is going to
move upwards. Let us assume that mass
, we cannot determine beforehand which mass is going to
move upwards. Let us assume that mass ![]() is going to move upwards:
if we are wrong in this assumption then we will simply obtain a negative
acceleration for this mass. The first mass is subject to an
upward force
is going to move upwards:
if we are wrong in this assumption then we will simply obtain a negative
acceleration for this mass. The first mass is subject to an
upward force ![]() , due to the tension in the string, and a downward
force
, due to the tension in the string, and a downward
force ![]() , due to gravity. These forces cause the mass to
move upwards with acceleration
, due to gravity. These forces cause the mass to
move upwards with acceleration
| (108) |
| (109) |
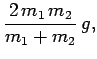 |
(110) | ||
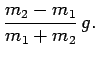 |
(111) |
Incidentally, the device pictured in Fig. 31 is called an Atwood machine, after the eighteenth Century English scientist George Atwood, who used it to ``slow down'' free-fall sufficiently to make accurate observations of this phenomena using the primitive time-keeping devices available in his day.