Mass and weight

The terms mass and weight are often confused with one another. However, in physics their meanings are quite distinct.

A body's mass is a measure of its inertia: i.e., its reluctance to deviate from uniform straight-line motion under the influence of external forces. According to Newton's second law, Eq. (94), if two objects of differing masses are acted upon by forces of the same magnitude then the resulting acceleration of the larger mass is less than that of the smaller mass. In other words, it is more difficult to force the larger mass to deviate from its preferred state of uniform motion in a straight line. Incidentally, the mass of a body is an intrinsic property of that body, and, therefore, does not change if the body is moved to a different place.

Figure 24: Weight

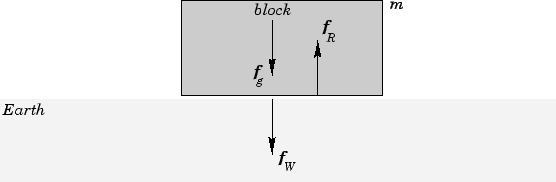
Imagine a block of granite resting on the surface of the Earth. See Fig. 24. The block experiences a downward force ${\bf f}_g$ due to the gravitational attraction of the Earth. This force is of magnitude $m g$, where $m$ is the mass of the block and $g$ is the acceleration due to gravity at the surface of the Earth. The block transmits this force to the ground below it, which is supporting it, and, thereby, preventing it from accelerating downwards. In other words, the block exerts a downward force ${\bf f}_W$, of magnitude $m g$, on the ground immediately beneath it. We usually refer to this force (or the magnitude of this force) as the weight of the block. According to Newton's third law, the ground below the block exerts an upward reaction force ${\bf f}_R$ on the block. This force is also of magnitude $m g$. Thus, the net force acting on the block is ${\bf f}_g + {\bf f}_R = {\bf0}$, which accounts for the fact that the block remains stationary.

Where, you might ask, is the equal and opposite reaction to the force of gravitational attraction ${\bf f}_g$ exerted by the Earth on the block of granite? It turns out that this reaction is exerted at the centre of the Earth. In other words, the Earth attracts the block of granite, and the block of granite attracts the Earth by an equal amount. However, since the Earth is far more massive than the block, the force exerted by the granite block at the centre of the Earth has no observable consequence.

So far, we have established that the weight $W$ of a body is the magnitude of the downward force it exerts on any object which supports it. Thus, $W=m g$, where $m$ is the mass of the body and $g$ is the local acceleration due to gravity. Since weight is a force, it is measured in newtons. A body's weight is location dependent, and is not, therefore, an intrinsic property of that body. For instance, a body weighing 10N on the surface of the Earth will only weigh about $3.8 {\rm N}$ on the surface of Mars, due to the weaker surface gravity of Mars relative to the Earth.

Figure 25: Weight in an elevator

Consider a block of mass $m$ resting on the floor of an elevator, as shown in Fig. 25. Suppose that the elevator is accelerating upwards with acceleration $a$. How does this acceleration affect the weight of the block? Of course, the block experiences a downward force $m g$ due to gravity. Let $W$ be the weight of the block: by definition, this is the size of the downward force exerted by the block on the floor of the elevator. From Newton's third law, the floor of the elevator exerts an upward reaction force of magnitude $W$ on the block. Let us apply Newton's second law, Eq. (94), to the motion of the block. The mass of the block is $m$, and its upward acceleration is $a$. Furthermore, the block is subject to two forces: a downward force $m g$ due to gravity, and an upward reaction force $W$. Hence,

$$W -m g = m a.$$ (95)

This equation can be rearranged to give

$$W = m (g+a).$$ (96)

Clearly, the upward acceleration of the elevator has the effect of increasing the weight $W$ of the block: for instance, if the elevator accelerates upwards at $g=9.81 {\rm m/s^2}$ then the weight of the block is doubled. Conversely, if the elevator accelerates downward (i.e., if $a$ becomes negative) then the weight of the block is reduced: for instance, if the elevator accelerates downward at $g/2$ then the weight of the block is halved. Incidentally, these weight changes could easily be measured by placing some scales between the block and the floor of the elevator.

Suppose that the downward acceleration of the elevator matches the acceleration due to gravity: i.e., $a=-g$. In this case, $W=0$. In other words, the block becomes weightless! This is the principle behind the so-called ``Vomit Comet'' used by NASA's Johnson Space Centre to train prospective astronauts in the effects of weightlessness. The ``Vomit Comet'' is actually a KC-135 (a predecessor of the Boeing 707 which is typically used for refueling military aircraft). The plane typically ascends to 30,000ft and then accelerates downwards at $g$ (i.e., drops like a stone) for about 20s, allowing its passengers to feel the effects of weightlessness during this period. All of the weightless scenes in the film Apollo 11 were shot in this manner.

Suppose, finally, that the downward acceleration of the elevator exceeds the acceleration due to gravity: i.e., $a<-g$. In this case, the block acquires a negative weight! What actually happens is that the block flies off the floor of the elevator and slams into the ceiling: when things have settled down, the block exerts an upward force (negative weight) $\vert W\vert$ on the ceiling of the elevator.