


Next: Worked example 11.1: Piston
Up: Oscillatory motion
Previous: The compound pendulum
Consider an object executing uniform circular motion of radius  . Let us set
up a cartesian coordinate system whose origin coincides with the centre of the circle,
and which is such that the motion is confined to the
. Let us set
up a cartesian coordinate system whose origin coincides with the centre of the circle,
and which is such that the motion is confined to the  -
- plane.
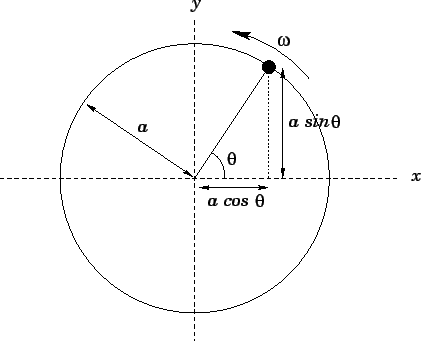
As illustrated in Fig. 99, the instantaneous position of the object can be conveniently
parameterized in terms of an angle
plane.
As illustrated in Fig. 99, the instantaneous position of the object can be conveniently
parameterized in terms of an angle  .
.
Figure 99:
Uniform circular motion.
 |
Since the object is executing uniform circular motion, we expect the angle  to increase
linearly with time. In other words, we can write
to increase
linearly with time. In other words, we can write
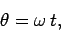 |
(536) |
where  is the angular rotation frequency (i.e., the number of radians through which the
object rotates per second). Here, it is assumed that
is the angular rotation frequency (i.e., the number of radians through which the
object rotates per second). Here, it is assumed that 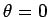 at
at  , for the sake of convenience.
, for the sake of convenience.
From simple trigonometry, the  - and
- and  -coordinates of the object can be written
-coordinates of the object can be written
respectively. Hence, combining the previous equations, we obtain
Here, use has been made of the trigonometric identity
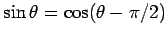 .
A comparison of the above two equations with the standard equation of simple harmonic motion,
Eq. (505), reveals that our object is executing simple harmonic motion simultaneously along both the
.
A comparison of the above two equations with the standard equation of simple harmonic motion,
Eq. (505), reveals that our object is executing simple harmonic motion simultaneously along both the
 - and the
- and the  -axes. Note, however, that these two motions are
-axes. Note, however, that these two motions are 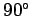 (i.e.,
(i.e., 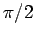 radians)
out of phase. Moreover, the amplitude of the motion equals the radius of the circle.
Clearly, there is a close relationship between simple harmonic motion
and circular motion.
radians)
out of phase. Moreover, the amplitude of the motion equals the radius of the circle.
Clearly, there is a close relationship between simple harmonic motion
and circular motion.



Next: Worked example 11.1: Piston
Up: Oscillatory motion
Previous: The compound pendulum
Richard Fitzpatrick
2006-02-02

![]() to increase
linearly with time. In other words, we can write
to increase
linearly with time. In other words, we can write
![]() - and
- and ![]() -coordinates of the object can be written
-coordinates of the object can be written