


Next: The torsion pendulum
Up: Oscillatory motion
Previous: Introduction
Let us reexamine the problem of a mass on a spring (see Sect. 5.6).
Consider a mass  which slides over a horizontal frictionless surface. Suppose that
the mass is attached
to a light horizontal spring whose other end is anchored to an immovable object. See
Fig. 42. Let
which slides over a horizontal frictionless surface. Suppose that
the mass is attached
to a light horizontal spring whose other end is anchored to an immovable object. See
Fig. 42. Let  be the extension of the spring: i.e., the difference between
the spring's actual length and its unstretched length. Obviously,
be the extension of the spring: i.e., the difference between
the spring's actual length and its unstretched length. Obviously,  can also be used as
a coordinate to determine the horizontal displacement of the mass.
can also be used as
a coordinate to determine the horizontal displacement of the mass.
The equilibrium state of the system corresponds to the situation where
the mass is at rest, and the spring is unextended (i.e.,  ).
In this state, zero net force acts on the mass, so there is no reason for it to start to move.
If the system is perturbed from this equilibrium state (i.e., if the mass is moved, so that the
spring becomes extended) then the mass experiences a restoring force given by Hooke's law:
).
In this state, zero net force acts on the mass, so there is no reason for it to start to move.
If the system is perturbed from this equilibrium state (i.e., if the mass is moved, so that the
spring becomes extended) then the mass experiences a restoring force given by Hooke's law:
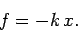 |
(503) |
Here, 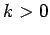 is the force constant of the spring. The negative sign indicates that
is the force constant of the spring. The negative sign indicates that 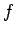 is indeed a restoring force.
Note that the magnitude of the restoring
force is directly proportional to the displacement of the system from equilibrium
(i.e.,
is indeed a restoring force.
Note that the magnitude of the restoring
force is directly proportional to the displacement of the system from equilibrium
(i.e.,  ). Of course, Hooke's law only holds for small spring extensions.
Hence, the displacement from equilibrium cannot be made too large.
The motion of this system is representative of the
motion of a wide range of systems when they are slightly disturbed from a stable equilibrium state.
). Of course, Hooke's law only holds for small spring extensions.
Hence, the displacement from equilibrium cannot be made too large.
The motion of this system is representative of the
motion of a wide range of systems when they are slightly disturbed from a stable equilibrium state.
Newton's second law gives following equation of motion for the system:
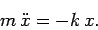 |
(504) |
This differential equation is known as the simple harmonic equation, and its solution has been known
for centuries. In fact, the solution is
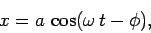 |
(505) |
where  ,
,  , and
, and 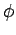 are constants. We can demonstrate that Eq. (505) is indeed a
solution of Eq. (504) by direct substitution. Substituting Eq. (505) into
Eq. (504), and recalling from calculus that
are constants. We can demonstrate that Eq. (505) is indeed a
solution of Eq. (504) by direct substitution. Substituting Eq. (505) into
Eq. (504), and recalling from calculus that
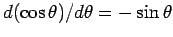 and
and
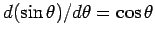 , we obtain
, we obtain
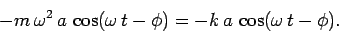 |
(506) |
It follows that Eq. (505) is the correct solution provided
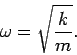 |
(507) |
Figure 95 shows a graph of  versus
versus  obtained from Eq. (505). The type of motion shown here is
called simple harmonic motion.
It can be seen that
the displacement
obtained from Eq. (505). The type of motion shown here is
called simple harmonic motion.
It can be seen that
the displacement  oscillates between
oscillates between 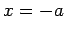 and
and 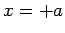 . Here,
. Here,  is termed the amplitude
of the oscillation. Moreover, the motion is periodic in time (i.e., it repeats exactly after
a certain time period has elapsed). In fact, the period is
is termed the amplitude
of the oscillation. Moreover, the motion is periodic in time (i.e., it repeats exactly after
a certain time period has elapsed). In fact, the period is
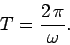 |
(508) |
This result is easily obtained from Eq. (505) by noting that 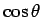 is a periodic function
of
is a periodic function
of  with
period
with
period 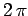 . The frequency of the motion (i.e., the number of oscillations completed per
second) is
. The frequency of the motion (i.e., the number of oscillations completed per
second) is
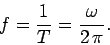 |
(509) |
It can be seen that  is the motion's angular frequency (i.e., the frequency
is the motion's angular frequency (i.e., the frequency
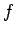 converted into radians per second).
Finally, the phase angle
converted into radians per second).
Finally, the phase angle 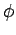 determines the times at which the oscillation attains its maximum amplitude,
determines the times at which the oscillation attains its maximum amplitude,
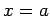 : in fact,
: in fact,
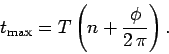 |
(510) |
Here, 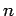 is an arbitrary integer.
is an arbitrary integer.
Table 4:
Simple harmonic motion.
|
|
Table 4 lists the displacement, velocity, and acceleration of the mass at various phases of the
simple harmonic cycle. The information contained in this table can easily be derived from the
simple harmonic equation, Eq. (505). Note that all of the non-zero values
shown in this table represent either the maximum or the minimum value taken by the quantity in question during the
oscillation cycle.
Figure 95:
Simple harmonic motion.
 |
We have seen that when a mass on a spring is disturbed from equilibrium it executes simple harmonic
motion about its equilibrium state. In physical terms, if the initial displacement is positive (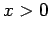 ) then the
restoring force overcompensates, and sends the system past the equilibrium state (
) then the
restoring force overcompensates, and sends the system past the equilibrium state ( ) to
negative displacement states (
) to
negative displacement states (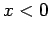 ). The restoring force again overcompensates, and sends the
system back through
). The restoring force again overcompensates, and sends the
system back through  to positive displacement states. The motion then repeats itself ad infinitum.
The frequency of the oscillation is determined by the spring stiffness,
to positive displacement states. The motion then repeats itself ad infinitum.
The frequency of the oscillation is determined by the spring stiffness, 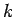 , and the system
inertia,
, and the system
inertia,  , via Eq. (507).
In contrast, the amplitude and phase angle of the oscillation are determined by the initial conditions.
Suppose that the instantaneous displacement and velocity of the mass at
, via Eq. (507).
In contrast, the amplitude and phase angle of the oscillation are determined by the initial conditions.
Suppose that the instantaneous displacement and velocity of the mass at  are
are 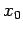 and
and 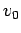 ,
respectively. It follows from Eq. (505) that
,
respectively. It follows from Eq. (505) that
Here, use has been made of the well-known identities
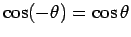 and
and
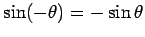 . Hence, we obtain
. Hence, we obtain
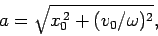 |
(513) |
and
 |
(514) |
since
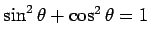 and
and
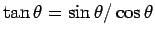 .
.
The kinetic energy of the system is written
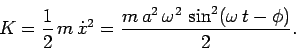 |
(515) |
Recall, from Sect. 5.6, that the potential energy takes the form
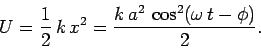 |
(516) |
Hence, the total energy can be written
 |
(517) |
since
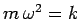 and
and
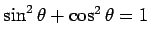 . Note that the
total energy is a constant of the motion, as expected for an isolated system. Moreover,
the energy is proportional to the amplitude squared of the motion.
It is clear, from the above expressions, that simple harmonic motion is characterized
by a constant backward and forward flow of energy between kinetic and potential components.
The kinetic energy attains its maximum value, and the potential energy attains
it minimum value, when the displacement is zero (i.e., when
. Note that the
total energy is a constant of the motion, as expected for an isolated system. Moreover,
the energy is proportional to the amplitude squared of the motion.
It is clear, from the above expressions, that simple harmonic motion is characterized
by a constant backward and forward flow of energy between kinetic and potential components.
The kinetic energy attains its maximum value, and the potential energy attains
it minimum value, when the displacement is zero (i.e., when  ). Likewise,
the potential energy attains its maximum value, and the kinetic energy attains
its minimum value, when the displacement is maximal (i.e., when
). Likewise,
the potential energy attains its maximum value, and the kinetic energy attains
its minimum value, when the displacement is maximal (i.e., when  ).
Note that the minimum value of
).
Note that the minimum value of 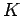 is zero, since the system is instantaneously at rest
when the displacement is maximal.
is zero, since the system is instantaneously at rest
when the displacement is maximal.



Next: The torsion pendulum
Up: Oscillatory motion
Previous: Introduction
Richard Fitzpatrick
2006-02-02
![]() ).
In this state, zero net force acts on the mass, so there is no reason for it to start to move.
If the system is perturbed from this equilibrium state (i.e., if the mass is moved, so that the
spring becomes extended) then the mass experiences a restoring force given by Hooke's law:
).
In this state, zero net force acts on the mass, so there is no reason for it to start to move.
If the system is perturbed from this equilibrium state (i.e., if the mass is moved, so that the
spring becomes extended) then the mass experiences a restoring force given by Hooke's law:
![]() versus
versus ![]() obtained from Eq. (505). The type of motion shown here is
called simple harmonic motion.
It can be seen that
the displacement
obtained from Eq. (505). The type of motion shown here is
called simple harmonic motion.
It can be seen that
the displacement ![]() oscillates between
oscillates between ![]() and
and ![]() . Here,
. Here, ![]() is termed the amplitude
of the oscillation. Moreover, the motion is periodic in time (i.e., it repeats exactly after
a certain time period has elapsed). In fact, the period is
is termed the amplitude
of the oscillation. Moreover, the motion is periodic in time (i.e., it repeats exactly after
a certain time period has elapsed). In fact, the period is
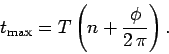
![]() ) then the
restoring force overcompensates, and sends the system past the equilibrium state (
) then the
restoring force overcompensates, and sends the system past the equilibrium state (![]() ) to
negative displacement states (
) to
negative displacement states (![]() ). The restoring force again overcompensates, and sends the
system back through
). The restoring force again overcompensates, and sends the
system back through ![]() to positive displacement states. The motion then repeats itself ad infinitum.
The frequency of the oscillation is determined by the spring stiffness,
to positive displacement states. The motion then repeats itself ad infinitum.
The frequency of the oscillation is determined by the spring stiffness, ![]() , and the system
inertia,
, and the system
inertia, ![]() , via Eq. (507).
In contrast, the amplitude and phase angle of the oscillation are determined by the initial conditions.
Suppose that the instantaneous displacement and velocity of the mass at
, via Eq. (507).
In contrast, the amplitude and phase angle of the oscillation are determined by the initial conditions.
Suppose that the instantaneous displacement and velocity of the mass at ![]() are
are ![]() and
and ![]() ,
respectively. It follows from Eq. (505) that
,
respectively. It follows from Eq. (505) that