


Next: The compound pendulum
Up: Oscillatory motion
Previous: The torsion pendulum
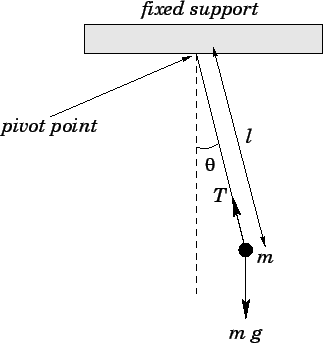
Consider a mass  suspended from a light inextensible string of length
suspended from a light inextensible string of length 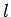 , such that the
mass is free to swing from side to side in a vertical plane, as shown in Fig. 97.
This setup is known as a simple pendulum.
Let
, such that the
mass is free to swing from side to side in a vertical plane, as shown in Fig. 97.
This setup is known as a simple pendulum.
Let  be the angle subtended between the string and
the downward vertical. Obviously, the equilibrium state of the simple pendulum corresponds to
the situation in which the mass is stationary and hanging vertically down (i.e.,
be the angle subtended between the string and
the downward vertical. Obviously, the equilibrium state of the simple pendulum corresponds to
the situation in which the mass is stationary and hanging vertically down (i.e., 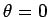 ).
The angular equation of motion of the pendulum is simply
).
The angular equation of motion of the pendulum is simply
 |
(523) |
where 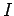 is the moment of inertia of the mass, and
is the moment of inertia of the mass, and 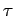 is the torque acting on the system. For the
case in hand, given that the mass is essentially a point particle, and is situated a distance
is the torque acting on the system. For the
case in hand, given that the mass is essentially a point particle, and is situated a distance 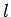 from
the axis of rotation (i.e., the pivot point), it is easily seen that
from
the axis of rotation (i.e., the pivot point), it is easily seen that 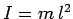 .
.
Figure 97:
A simple pendulum.
 |
The two forces acting on the mass are the downward gravitational force,  , and the tension,
, and the tension, 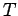 , in the string.
Note, however, that the tension makes no contribution to the torque, since its line of action clearly passes
through the pivot point. From simple trigonometry,
the line of action of the gravitational force passes a distance
, in the string.
Note, however, that the tension makes no contribution to the torque, since its line of action clearly passes
through the pivot point. From simple trigonometry,
the line of action of the gravitational force passes a distance 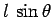 from the
pivot point. Hence, the magnitude of the gravitational torque is
from the
pivot point. Hence, the magnitude of the gravitational torque is
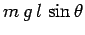 .
Moreover, the gravitational torque is a restoring torque: i.e., if the mass is
displaced slightly from its equilibrium state (i.e.,
.
Moreover, the gravitational torque is a restoring torque: i.e., if the mass is
displaced slightly from its equilibrium state (i.e., 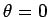 ) then the gravitational force clearly acts
to push the mass back toward that state. Thus, we can write
) then the gravitational force clearly acts
to push the mass back toward that state. Thus, we can write
 |
(524) |
Combining the previous two equations, we obtain the following angular equation of motion of the pendulum:
 |
(525) |
Unfortunately, this is not the simple harmonic equation. Indeed, the above equation possesses no
closed solution which can be expressed in terms of simple functions.
Suppose that
we restrict our attention to relatively small deviations from the equilibrium state. In other
words, suppose that the angle  is constrained to take fairly small values. We know,
from trigonometry, that for
is constrained to take fairly small values. We know,
from trigonometry, that for 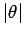 less than about
less than about 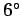 it is a good approximation to
write
it is a good approximation to
write
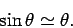 |
(526) |
Hence, in the small angle limit, Eq. (525) reduces to
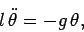 |
(527) |
which is in the familiar form of a simple harmonic equation. Comparing with our original simple harmonic
equation, Eq. (504), and its solution, we conclude that the angular frequency of small amplitude
oscillations of a simple pendulum is given by
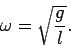 |
(528) |
In this case, the pendulum frequency is dependent only on the length of the pendulum and the local gravitational acceleration,
and is independent of the mass of the pendulum and the amplitude of the pendulum swings (provided that
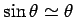 remains
a good approximation). Historically,
the simple pendulum was the basis of virtually all accurate time-keeping devices before the
advent of electronic clocks. Simple pendulums can also be used to measure local variations in
remains
a good approximation). Historically,
the simple pendulum was the basis of virtually all accurate time-keeping devices before the
advent of electronic clocks. Simple pendulums can also be used to measure local variations in 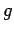 .
.



Next: The compound pendulum
Up: Oscillatory motion
Previous: The torsion pendulum
Richard Fitzpatrick
2006-02-02
![]() , and the tension,
, and the tension, ![]() , in the string.
Note, however, that the tension makes no contribution to the torque, since its line of action clearly passes
through the pivot point. From simple trigonometry,
the line of action of the gravitational force passes a distance
, in the string.
Note, however, that the tension makes no contribution to the torque, since its line of action clearly passes
through the pivot point. From simple trigonometry,
the line of action of the gravitational force passes a distance ![]() from the
pivot point. Hence, the magnitude of the gravitational torque is
from the
pivot point. Hence, the magnitude of the gravitational torque is
![]() .
Moreover, the gravitational torque is a restoring torque: i.e., if the mass is
displaced slightly from its equilibrium state (i.e.,
.
Moreover, the gravitational torque is a restoring torque: i.e., if the mass is
displaced slightly from its equilibrium state (i.e., ![]() ) then the gravitational force clearly acts
to push the mass back toward that state. Thus, we can write
) then the gravitational force clearly acts
to push the mass back toward that state. Thus, we can write
![]() is constrained to take fairly small values. We know,
from trigonometry, that for
is constrained to take fairly small values. We know,
from trigonometry, that for ![]() less than about
less than about ![]() it is a good approximation to
write
it is a good approximation to
write