The physics of baseball

Baseball players know from experience that there is a ``sweet spot'' on a baseball bat, about 17cm from the end of the barrel, where the shock of impact with the ball, as felt by the hands, is minimized. In fact, if the ball strikes the bat exactly on the ``sweet spot'' then the hitter is almost unaware of the collision. Conversely, if the ball strikes the bat well away from the ``sweet spot'' then the impact is felt as a painful jarring of the hands.

The existence of a ``sweet spot'' on a baseball bat is just a consequence of rotational dynamics. Let us analyze this problem. Consider the schematic baseball bat shown in Fig. 82. Let $M$ be the mass of the bat, and let $l$ be its length. Suppose that the bat pivots about a fixed point located at one of its ends. Let the centre of mass of the bat be located a distance $b$ from the pivot point. Finally, suppose that the ball strikes the bat a distance $h$ from the pivot point.

The collision between the bat and the ball can be modeled as equal and opposite impulses, $J$, applied to each object at the time of the collision (see Sect. 6.5). At the same time, equal and opposite impulses $J'$ are applied to the pivot and the bat, as shown in Fig. 82. If the pivot actually corresponds to a hitter's hands then the latter impulse gives rise to the painful jarring sensation felt when the ball is not struck properly.

Figure 82: A schematic baseball bat.

We saw earlier that in a general multi-component system--which includes an extended body such as a baseball bat--the motion of the centre of mass takes a particularly simple form (see Sect. 6.3). To be more exact, the motion of the centre of mass is equivalent to that of the point particle obtained by concentrating the whole mass of the system at the centre of mass, and then allowing all of the external forces acting on the system to act upon that mass. Let us use this idea to analyze the effect of the collision with the ball on the motion of the bat's centre of mass. The centre of mass of the bat acts like a point particle of mass $M$ which is subject to the two impulses, $J$ and $J'$ (which are applied simultaneously). If $v$ is the instantaneous velocity of the centre of mass then the change in momentum of this point due to the action of the two impulses is simply

$$M {\mit\Delta} v = -J - J'.$$ (383)

The minus signs on the right-hand side of the above equation follow from the fact that the impulses are oppositely directed to $v$ in Fig. 82.

Note that in order to specify the instantaneous state of an extended body we must do more than just specify the location of the body's centre of mass. Indeed, since the body can rotate about its centre of mass, we must also specify its orientation in space. Thus, in order to follow the motion of an extended body, we must not only follow the translational motion of its centre of mass, but also the body's rotational motion about this point (or any other convenient reference point located within the body).

Consider the rotational motion of the bat shown in Fig. 82 about a perpendicular (to the bat) axis passing through the pivot point. This motion satisfies

$$I \frac{d\omega}{dt} = \tau,$$ (384)

where $I$ is the moment of inertia of the bat, $\omega$ is its instantaneous angular velocity, and $\tau$ is the applied torque. The bat is actually subject to an impulsive torque (i.e., a torque which only lasts for a short period in time) at the time of the collision with the ball. Defining the angular impulse $K$ associated with an impulsive torque $\tau$ in much the same manner as we earlier defined the impulse associated with an impulsive force (see Sect. 6.5), we obtain

$$K = \int^t \tau dt.$$ (385)

It follows that we can integrate Eq. (384) over the time of the collision to find

$$I {\mit\Delta}\omega = K,$$ (386)

where ${\mit\Delta}\omega$ is the change in angular velocity of the bat due to the collision with the ball.

Now, the torque associated with a given force is equal to the magnitude of the force times the length of the lever arm. Thus, it stands to reason that the angular impulse, $K$, associated with an impulse, $J$, is simply

$$K = J x,$$ (387)

where $x$ is the perpendicular distance from the line of action of the impulse to the axis of rotation. Hence, the angular impulses associated with the two impulses, $J$ and $J'$, to which the bat is subject when it collides with the ball, are $J h$ and $0$, respectively. The latter angular impulse is zero since the point of application of the associated impulse coincides with the pivot point, and so the length of the lever arm is zero. It follows that Eq. (386) can be written

$$I {\mit\Delta}\omega = -J h.$$ (388)

The minus sign comes from the fact that the impulse $J$ is oppositely directed to the angular velocity in Fig. 82.

Now, the relationship between the instantaneous velocity of the bat's centre of mass and the bat's instantaneous angular velocity is simply

$$v = b \omega.$$ (389)

Hence, Eq. (383) can be rewritten

$$M b {\mit\Delta} \omega = -J - J'.$$ (390)

Equations (388) and (390) can be combined to yield

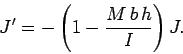$$J' = -\left(1 - \frac{M b h}{I}\right) J.$$ (391)

' The above expression specifies the magnitude of the impulse $J'$ applied to the hitter's hands terms of the magnitude of the impulse $J$ applied to the ball.

Let us crudely model the bat as a uniform rod of length $l$ and mass $M$. It follows, by symmetry, that the centre of mass of the bat lies at its half-way point: i.e.,

$$b = \frac{l}{2}.$$ (392)

Moreover, the moment of inertia of the bat about a perpendicular axis passing through one of its ends is

$$I = \frac{1}{3} M l^2$$ (393)

(this is a standard result). Combining the previous three equations, we obtain

$$J' = -\left(1 - \frac{3 h}{2 l}\right) J=-\left(1 - \frac{h}{h_0}\right) J,$$ (394)

where

$$h_0 = \frac{2}{3} l.$$ (395)

Clearly, if $h=h_0$ then no matter how hard the ball is hit (i.e., no matter how large we make $J$) zero impulse is applied to the hitter's hands. We conclude that the ``sweet spot''--or, in scientific terms, the centre of percussion--of a uniform baseball bat lies two-thirds of the way down the bat from the hitter's end. If we adopt a more realistic model of a baseball bat, in which the bat is tapered such that the majority of its weight is located at its hitting end, we can easily demonstrate that the centre of percussion is shifted further away from the hitter (i.e., it is more that two-thirds of the way along the bat).