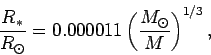

Next: About this document ...
Up: Quantum statistics
Previous: The Chandrasekhar limit
At stellar densities which greatly exceed white-dwarf densities, the
extreme pressures cause electrons to combine with
protons to form neutrons. Thus, any star which collapses to such an extent that
its
radius becomes significantly less than that characteristic
of a white-dwarf
is effectively transformed into a gas of
neutrons. Eventually, the mean separation between the neutrons becomes
comparable with their de Broglie wavelength. At this point, it is possible
for the degeneracy pressure of the neutrons to halt the collapse of the star.
A star which is maintained against gravity in this manner is called
a neutron star.
Neutrons stars can be analyzed in a very similar manner to
white-dwarf stars. In fact, the previous analysis can be simply modified
by letting
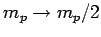 and
and
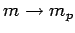 .
Thus,
we conclude that
non-relativistic neutrons stars satisfy the mass-radius law:
.
Thus,
we conclude that
non-relativistic neutrons stars satisfy the mass-radius law:
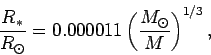 |
(708) |
It follows that the radius of a typical solar mass neutron star is
a mere 10km. In 1967 Antony Hewish and
Jocelyn Bell discovered a class of compact radio sources, called pulsars,
which emit
extremely regular pulses of radio waves. Pulsars have subsequently
been identified as
rotating neutron stars. To date, many hundreds of these objects have been
observed.
When relativistic effects are taken into account,
it is found that there is
a critical mass above which a neutron star cannot be maintained against
gravity.
According to our analysis,
this critical mass, which is known as the Oppenheimer-Volkoff
limit, is given by
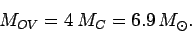 |
(709) |
A more realistic calculation, which
does not assume constant density, does not
treat the neutrons as point particles, and takes general relativity into account,
gives a somewhat lower value of
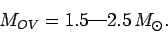 |
(710) |
A star whose mass exceeds the Oppenheimer-Volkoff
limit cannot be maintained against gravity by degeneracy pressure, and
must ultimately collapse to form a black-hole.


Next: About this document ...
Up: Quantum statistics
Previous: The Chandrasekhar limit
Richard Fitzpatrick
2006-02-02
![]() and
and
![]() .
Thus,
we conclude that
non-relativistic neutrons stars satisfy the mass-radius law:
.
Thus,
we conclude that
non-relativistic neutrons stars satisfy the mass-radius law: