


Next: White-dwarf stars
Up: Quantum statistics
Previous: The Stefan-Boltzmann law
The conduction electrons in a metal are non-localized (i.e., they are
not tied to any particular atoms). In conventional metals, each atom contributes
a single such electron. To a first approximation, it is possible
to neglect the mutual interaction of the conduction electrons, since this
interaction
is largely shielded out by the stationary atoms. The conduction electrons
can, therefore, be treated as an ideal gas. However, the concentration of
such electrons in a metal far exceeds the concentration of
particles in a conventional gas. It is, therefore, not surprising that
conduction electrons cannot normally be analyzed using classical statistics:
in fact, they are subject to Fermi-Dirac statistics
(since electrons are fermions).
Recall, from Sect. 8.5, that the mean number of particles occupying
state 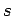 (energy
(energy 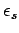 ) is given by
) is given by
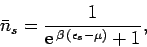 |
(662) |
according to the Fermi-Dirac distribution. Here,
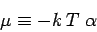 |
(663) |
is termed the Fermi energy of the system. This energy is
determined by the condition that
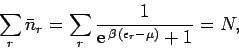 |
(664) |
where  is the total number of particles contained in the volume
is the total number of particles contained in the volume 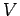 .
It is clear, from the above equation, that the Fermi energy
.
It is clear, from the above equation, that the Fermi energy 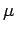 is generally
a function of the temperature
is generally
a function of the temperature  .
.
Let us investigate the behaviour of the Fermi function
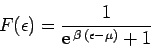 |
(665) |
as 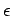 varies. Here, the energy is measured from
its lowest possible value
varies. Here, the energy is measured from
its lowest possible value 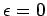 . If the Fermi energy
. If the Fermi energy 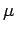 is
such that
is
such that
 then
then
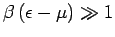 ,
and
,
and 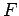 reduces to the Maxwell-Boltzmann distribution. However,
for the case of conduction electrons in a metal we are interested in
the opposite limit, where
reduces to the Maxwell-Boltzmann distribution. However,
for the case of conduction electrons in a metal we are interested in
the opposite limit, where
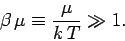 |
(666) |
In this limit, if
 then
then
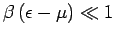 ,
so that
,
so that 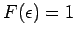 . On the other hand, if
. On the other hand, if
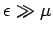 then
then
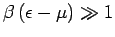 , so that
, so that
![$F(\epsilon)=
\exp[-\beta\,(\epsilon-\mu)]$](img1538.png) falls off exponentially with increasing
falls off exponentially with increasing
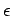 , just like a classical Boltzmann distribution. Note that
, just like a classical Boltzmann distribution. Note that
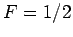 when
when 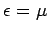 . The transition region in which
. The transition region in which 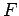 goes from
a value close to unity to a value close to zero corresponds to an
energy interval of order
goes from
a value close to unity to a value close to zero corresponds to an
energy interval of order 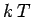 , centred on
, centred on 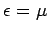 . This is
illustrated in Fig. 10.
. This is
illustrated in Fig. 10.
Figure 10:
The Fermi function.
 |
In the limit as
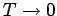 , the transition region becomes
infinitesimally narrow. In this case,
, the transition region becomes
infinitesimally narrow. In this case, 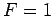 for
for 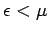 and
and
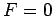 for
for 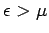 , as illustrated in Fig. 10.
This is an obvious result, since when
, as illustrated in Fig. 10.
This is an obvious result, since when 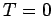 the conduction
electrons attain their lowest energy, or ground-state, configuration.
Since the Pauli exclusion principle requires that there be no
more than one electron per single-particle quantum state, the lowest
energy configuration is obtained by piling
electrons into the lowest available unoccupied states until all of
the electrons are used up. Thus, the last electron added to the
pile has quite a considerable energy,
the conduction
electrons attain their lowest energy, or ground-state, configuration.
Since the Pauli exclusion principle requires that there be no
more than one electron per single-particle quantum state, the lowest
energy configuration is obtained by piling
electrons into the lowest available unoccupied states until all of
the electrons are used up. Thus, the last electron added to the
pile has quite a considerable energy, 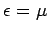 , since all of the
lower energy states are already occupied. Clearly, the exclusion principle
implies that a Fermi-Dirac gas possesses a large mean energy, even at absolute
zero.
, since all of the
lower energy states are already occupied. Clearly, the exclusion principle
implies that a Fermi-Dirac gas possesses a large mean energy, even at absolute
zero.
Let us calculate the Fermi energy 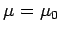 of a Fermi-Dirac
gas at
of a Fermi-Dirac
gas at 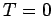 . The energy of each particle is related to its
momentum
. The energy of each particle is related to its
momentum
 via
via
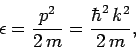 |
(667) |
where  is the de Broglie wave-vector. At
is the de Broglie wave-vector. At 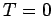 all quantum states
whose energy is less than the Fermi energy
all quantum states
whose energy is less than the Fermi energy 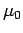 are filled. The
Fermi energy corresponds to a Fermi momentum
are filled. The
Fermi energy corresponds to a Fermi momentum
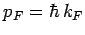 which
is such that
which
is such that
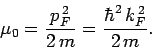 |
(668) |
Thus, at 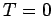 all quantum states with
all quantum states with 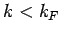 are filled, and all
those with
are filled, and all
those with 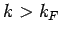 are empty.
are empty.
Now, we know, by analogy with Eq. (514), that there are
 allowable translational states per unit volume of
allowable translational states per unit volume of  -space. The volume of
the sphere of radius
-space. The volume of
the sphere of radius  in
in  -space is
-space is
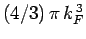 . It
follows that the Fermi sphere of radius
. It
follows that the Fermi sphere of radius  contains
contains
 translational states. The number of
quantum states inside the sphere is twice this, because electrons
possess two possible spin states for every possible translational state. Since the
total number of occupied states (i.e., the total number of quantum
states inside the Fermi sphere) must equal the total number of particles
in the gas, it follows that
translational states. The number of
quantum states inside the sphere is twice this, because electrons
possess two possible spin states for every possible translational state. Since the
total number of occupied states (i.e., the total number of quantum
states inside the Fermi sphere) must equal the total number of particles
in the gas, it follows that
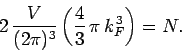 |
(669) |
The above expression can be rearranged to
give
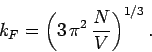 |
(670) |
Hence,
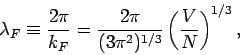 |
(671) |
which implies that the de Broglie wavelength 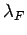 corresponding to the Fermi energy is of order the mean separation
between particles
corresponding to the Fermi energy is of order the mean separation
between particles 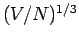 . All quantum states with de Broglie
wavelengths
. All quantum states with de Broglie
wavelengths
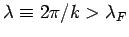 are occupied
at
are occupied
at 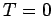 , whereas all those with
, whereas all those with
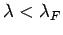 are empty.
are empty.
According to Eq. (668), the Fermi energy at 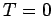 takes the form
takes the form
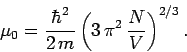 |
(672) |
It is easily demonstrated that 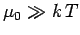 for conventional metals
at room temperature.
for conventional metals
at room temperature.
The majority of the conduction electrons in a metal occupy a
band of completely filled states with energies far below the Fermi
energy. In many cases, such electrons have very little effect
on the macroscopic properties of the metal. Consider, for example, the
contribution of the conduction electrons to the specific heat of the metal.
The heat capacity 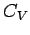 at constant volume of these electrons can
be calculated from a knowledge of their mean energy
at constant volume of these electrons can
be calculated from a knowledge of their mean energy 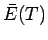 as a
function of
as a
function of  : i.e.,
: i.e.,
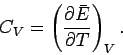 |
(673) |
If the electrons obeyed classical Maxwell-Boltzmann statistics, so that
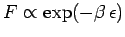 for all electrons, then the
equipartition theorem would give
for all electrons, then the
equipartition theorem would give
However, the actual situation, in which 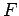 has the form shown in Fig. 10,
is very different. A small change in
has the form shown in Fig. 10,
is very different. A small change in  does not affect the
mean energies of
the majority of the electrons, with
does not affect the
mean energies of
the majority of the electrons, with
 , since these electrons
lie in states which are completely filled, and remain so when the temperature
is changed. It follows that these electrons contribute nothing whatsoever to
the heat capacity. On the other hand, the relatively small number of
electrons
, since these electrons
lie in states which are completely filled, and remain so when the temperature
is changed. It follows that these electrons contribute nothing whatsoever to
the heat capacity. On the other hand, the relatively small number of
electrons  in the energy range of order
in the energy range of order 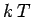 , centred on the
Fermi energy, in which
, centred on the
Fermi energy, in which 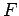 is significantly different from 0 and 1,
do contribute to the specific heat. In the tail end of this region
is significantly different from 0 and 1,
do contribute to the specific heat. In the tail end of this region
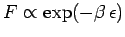 , so the
distribution reverts to a Maxwell-Boltzmann distribution.
Hence, from Eq. (675),
we expect each electron in this region to contribute roughly an amount
, so the
distribution reverts to a Maxwell-Boltzmann distribution.
Hence, from Eq. (675),
we expect each electron in this region to contribute roughly an amount
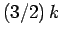 to the heat capacity. Hence, the heat capacity
can be written
to the heat capacity. Hence, the heat capacity
can be written
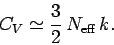 |
(676) |
However, since only a fraction 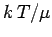 of the total conduction
electrons lie in the tail region of the Fermi-Dirac distribution, we
expect
of the total conduction
electrons lie in the tail region of the Fermi-Dirac distribution, we
expect
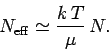 |
(677) |
It follows that
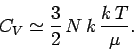 |
(678) |
Since 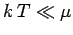 in conventional metals, the molar specific heat of
the conduction electrons is clearly very much less than the classical value
in conventional metals, the molar specific heat of
the conduction electrons is clearly very much less than the classical value
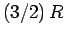 . This accounts for the fact that
the molar specific heat capacities of metals at room temperature are
about the same as those of insulators. Before the advent of
quantum mechanics, the classical theory predicted incorrectly that the
presence of conduction electrons should raise the heat capacities of
metals by 50 percent [i.e.,
. This accounts for the fact that
the molar specific heat capacities of metals at room temperature are
about the same as those of insulators. Before the advent of
quantum mechanics, the classical theory predicted incorrectly that the
presence of conduction electrons should raise the heat capacities of
metals by 50 percent [i.e., 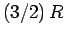 ] compared to those of insulators.
] compared to those of insulators.
Note that the specific heat (678) is not temperature independent.
In fact, using the superscript 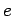 to denote the electronic
specific heat, the molar specific heat can be written
to denote the electronic
specific heat, the molar specific heat can be written
 |
(679) |
where 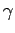 is a (positive) constant of proportionality.
At room temperature
is a (positive) constant of proportionality.
At room temperature 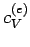 is completely masked by the much
larger specific heat
is completely masked by the much
larger specific heat 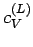 due to lattice vibrations. However, at
very low temperatures
due to lattice vibrations. However, at
very low temperatures
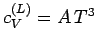 , where
, where  is a (positive)
constant of proportionality (see Sect. 7.12). Clearly,
at low temperatures
is a (positive)
constant of proportionality (see Sect. 7.12). Clearly,
at low temperatures
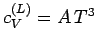 approaches zero far more rapidly that
the electronic specific heat, as
approaches zero far more rapidly that
the electronic specific heat, as  is reduced. Hence, it should be possible
to measure the electronic contribution to the molar specific
heat at low temperatures.
is reduced. Hence, it should be possible
to measure the electronic contribution to the molar specific
heat at low temperatures.
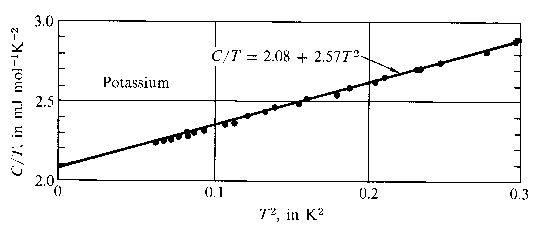
The total molar specific heat of a metal at low temperatures takes the
form
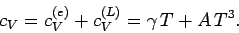 |
(680) |
Hence,
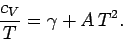 |
(681) |
If follows that a plot of 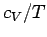 versus
versus 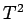 should yield a
straight line whose intercept on the vertical axis gives the
coefficient
should yield a
straight line whose intercept on the vertical axis gives the
coefficient 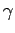 . Figure 11 shows such a plot.
The fact that a good straight line is obtained verifies that the temperature
dependence of the heat capacity predicted by Eq. (680) is indeed
correct.
. Figure 11 shows such a plot.
The fact that a good straight line is obtained verifies that the temperature
dependence of the heat capacity predicted by Eq. (680) is indeed
correct.
Figure 11:
The low temperature heat capacity of potassium, plotted as  versus
versus
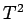 . From C. Kittel, and H. Kroemer, Themal physics (W.H. Freeman & co., New York NY, 1980).
. From C. Kittel, and H. Kroemer, Themal physics (W.H. Freeman & co., New York NY, 1980).
 |



Next: White-dwarf stars
Up: Quantum statistics
Previous: The Stefan-Boltzmann law
Richard Fitzpatrick
2006-02-02
![]() (energy
(energy ![]() ) is given by
) is given by
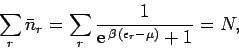
![]() , the transition region becomes
infinitesimally narrow. In this case,
, the transition region becomes
infinitesimally narrow. In this case, ![]() for
for ![]() and
and
![]() for
for ![]() , as illustrated in Fig. 10.
This is an obvious result, since when
, as illustrated in Fig. 10.
This is an obvious result, since when ![]() the conduction
electrons attain their lowest energy, or ground-state, configuration.
Since the Pauli exclusion principle requires that there be no
more than one electron per single-particle quantum state, the lowest
energy configuration is obtained by piling
electrons into the lowest available unoccupied states until all of
the electrons are used up. Thus, the last electron added to the
pile has quite a considerable energy,
the conduction
electrons attain their lowest energy, or ground-state, configuration.
Since the Pauli exclusion principle requires that there be no
more than one electron per single-particle quantum state, the lowest
energy configuration is obtained by piling
electrons into the lowest available unoccupied states until all of
the electrons are used up. Thus, the last electron added to the
pile has quite a considerable energy, ![]() , since all of the
lower energy states are already occupied. Clearly, the exclusion principle
implies that a Fermi-Dirac gas possesses a large mean energy, even at absolute
zero.
, since all of the
lower energy states are already occupied. Clearly, the exclusion principle
implies that a Fermi-Dirac gas possesses a large mean energy, even at absolute
zero.
![]() of a Fermi-Dirac
gas at
of a Fermi-Dirac
gas at ![]() . The energy of each particle is related to its
momentum
. The energy of each particle is related to its
momentum
![]() via
via
![]() allowable translational states per unit volume of
allowable translational states per unit volume of ![]() -space. The volume of
the sphere of radius
-space. The volume of
the sphere of radius ![]() in
in ![]() -space is
-space is
![]() . It
follows that the Fermi sphere of radius
. It
follows that the Fermi sphere of radius ![]() contains
contains
![]() translational states. The number of
quantum states inside the sphere is twice this, because electrons
possess two possible spin states for every possible translational state. Since the
total number of occupied states (i.e., the total number of quantum
states inside the Fermi sphere) must equal the total number of particles
in the gas, it follows that
translational states. The number of
quantum states inside the sphere is twice this, because electrons
possess two possible spin states for every possible translational state. Since the
total number of occupied states (i.e., the total number of quantum
states inside the Fermi sphere) must equal the total number of particles
in the gas, it follows that
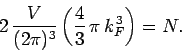
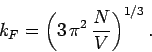
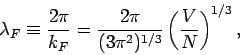
![]() takes the form
takes the form
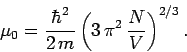
![]() at constant volume of these electrons can
be calculated from a knowledge of their mean energy
at constant volume of these electrons can
be calculated from a knowledge of their mean energy ![]() as a
function of
as a
function of ![]() : i.e.,
: i.e.,
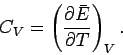
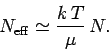
![]() in conventional metals, the molar specific heat of
the conduction electrons is clearly very much less than the classical value
in conventional metals, the molar specific heat of
the conduction electrons is clearly very much less than the classical value
![]() . This accounts for the fact that
the molar specific heat capacities of metals at room temperature are
about the same as those of insulators. Before the advent of
quantum mechanics, the classical theory predicted incorrectly that the
presence of conduction electrons should raise the heat capacities of
metals by 50 percent [i.e.,
. This accounts for the fact that
the molar specific heat capacities of metals at room temperature are
about the same as those of insulators. Before the advent of
quantum mechanics, the classical theory predicted incorrectly that the
presence of conduction electrons should raise the heat capacities of
metals by 50 percent [i.e., ![]() ] compared to those of insulators.
] compared to those of insulators.
![]() to denote the electronic
specific heat, the molar specific heat can be written
to denote the electronic
specific heat, the molar specific heat can be written
