


Next: Applications of statistical thermodynamics
Up: Classical thermodynamics
Previous: Heat engines
Let us now move on to consider refrigerators. An idealized
refrigerator is an engine
which extracts heat from a cold heat reservoir (temperature  , say) and rejects it
to a somewhat hotter heat reservoir, which is usually the environment (temperature
, say) and rejects it
to a somewhat hotter heat reservoir, which is usually the environment (temperature
 , say). To make this machine work we always have to do some external
work on the engine. For instance, the refrigerator in your home contains a small
electric pump which does work on the freon (or whatever) in the cooling
circuit. We can see that, in fact, a refrigerator is just a heat engine run
in reverse. Hence, we can immediately carry over most of our heat engine
analysis. Let
, say). To make this machine work we always have to do some external
work on the engine. For instance, the refrigerator in your home contains a small
electric pump which does work on the freon (or whatever) in the cooling
circuit. We can see that, in fact, a refrigerator is just a heat engine run
in reverse. Hence, we can immediately carry over most of our heat engine
analysis. Let 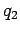 be the heat absorbed per cycle from the colder reservoir,
be the heat absorbed per cycle from the colder reservoir,
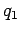 the heat rejected per cycle into the hotter reservoir, and
the heat rejected per cycle into the hotter reservoir, and  the
external work done
per cycle on the engine. The first law of thermodynamics tells us that
the
external work done
per cycle on the engine. The first law of thermodynamics tells us that
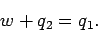 |
(364) |
The second law says that
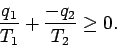 |
(365) |
We can combine these two laws to give
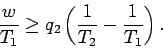 |
(366) |
The most sensible way of defining the efficiency of a refrigerator is as
the ratio of the heat extracted per cycle from the cold reservoir to
the work done per cycle on the engine. With this definition
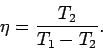 |
(367) |
We can see that this efficiency is, in general, greater than unity. In other
words, for one joule of work done on the engine, or pump, more than one
joule of energy is extracted from whatever it is
we are cooling. Clearly, refrigerators
are intrinsically very efficient devices. Domestic refrigerators cool stuff down
to about 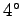 C (277
C (277 K) and reject heat to the environment
at about
K) and reject heat to the environment
at about 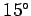 C (288
C (288 K). The maximum theoretical efficiency of
such devices is
K). The maximum theoretical efficiency of
such devices is
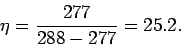 |
(368) |
So, for every joule of electricity we put into a refrigerator we can extract up
to 25 joules of heat from its contents.



Next: Applications of statistical thermodynamics
Up: Classical thermodynamics
Previous: Heat engines
Richard Fitzpatrick
2006-02-02