


Next: Statistical thermodynamics
Up: Heat and work
Previous: Quasi-static processes
Exact and inexact differentials
In our investigation of heat and work we have come across
various infinitesimal objects such as 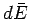 and
and
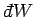 .
It is instructive to examine these infinitesimals more closely.
.
It is instructive to examine these infinitesimals more closely.
Consider the purely mathematical problem where 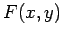 is some general
function of two
independent variables
is some general
function of two
independent variables 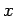 and
and 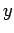 . Consider the change in
. Consider the change in 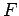 in
going from the point
in
going from the point 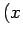 ,
, 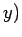 in the
in the 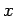 -
-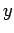 plane to the neighbouring point
(
plane to the neighbouring point
(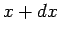 ,
, 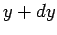 ). This is given by
). This is given by
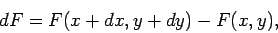 |
(135) |
which can also be written
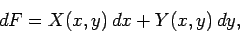 |
(136) |
where
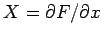 and
and
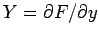 . Clearly,
. Clearly, 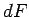 is
simply the infinitesimal difference between two adjacent values of the function
is
simply the infinitesimal difference between two adjacent values of the function 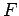 .
This type of infinitesimal quantity is termed an exact differential to
distinguish it from another type to be discussed presently.
If we move in the
.
This type of infinitesimal quantity is termed an exact differential to
distinguish it from another type to be discussed presently.
If we move in the 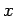 -
-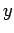 plane from an initial point
plane from an initial point 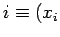 ,
, 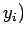 to a final point
to a final point 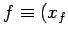 ,
, 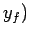 then the corresponding change in
then the corresponding change in 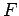 is
given by
is
given by
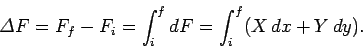 |
(137) |
Note that since the difference on the left-hand side depends only on the initial
and final points, the integral on the right-hand side can only depend on
these points as well.
In other words, the value of the
integral is independent of the path taken in going from the initial to the final
point. This is the distinguishing feature of an exact differential.
Consider an integral taken around a closed circuit in the 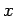 -
-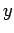 plane. In this
case, the initial and final points correspond to the same point, so the difference
plane. In this
case, the initial and final points correspond to the same point, so the difference
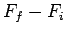 is clearly zero. It follows that the integral of an exact differential
over a closed circuit is always zero:
is clearly zero. It follows that the integral of an exact differential
over a closed circuit is always zero:
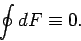 |
(138) |
Of course, not every infinitesimal quantity is an exact differential. Consider
the infinitesimal object
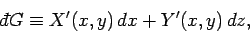 |
(139) |
where 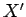 and
and  are two
general functions of
are two
general functions of 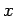 and
and 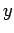 . It is easy to test whether or not
an infinitesimal quantity is an exact differential. Consider the expression
(136).
It is clear that since
. It is easy to test whether or not
an infinitesimal quantity is an exact differential. Consider the expression
(136).
It is clear that since
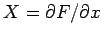 and
and
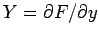 then
then
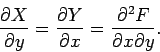 |
(140) |
Thus,
if
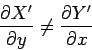 |
(141) |
(as is assumed to be the case), then
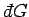 cannot be an exact differential, and
is instead termed an inexact differential.
The special symbol
cannot be an exact differential, and
is instead termed an inexact differential.
The special symbol
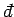 is used to denote an inexact differential.
Consider the integral of
is used to denote an inexact differential.
Consider the integral of
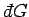 over some path in the
over some path in the 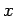 -
-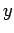 plane. In general, it is not true
that
plane. In general, it is not true
that
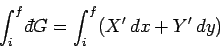 |
(142) |
is independent of the path taken between the initial and final points.
This is the distinguishing feature of an inexact differential. In particular,
the integral of an inexact differential around a closed circuit is not necessarily
zero, so
 |
(143) |
Consider, for the moment, the solution of
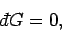 |
(144) |
which reduces to the ordinary differential equation
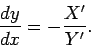 |
(145) |
Since the right-hand side is a known function of 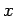 and
and 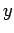 , the above
equation defines
a definite direction (i.e., gradient) at each point in the
, the above
equation defines
a definite direction (i.e., gradient) at each point in the 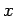 -
-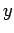 plane. The
solution simply consists of drawing a system of curves in the
plane. The
solution simply consists of drawing a system of curves in the
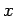 -
-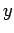 plane such that at any point the tangent to the curve is as specified
in Eq. (145). This defines a set of curves which can be written
plane such that at any point the tangent to the curve is as specified
in Eq. (145). This defines a set of curves which can be written
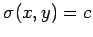 , where
, where 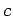 is a labeling parameter.
It follows that
is a labeling parameter.
It follows that
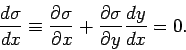 |
(146) |
The elimination of 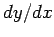 between Eqs. (145) and (146) yields
between Eqs. (145) and (146) yields
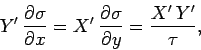 |
(147) |
where  is function of
is function of 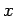 and
and 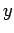 . The above equation could equally
well be written
. The above equation could equally
well be written
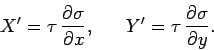 |
(148) |
Inserting Eq. (148) into Eq. (139) gives
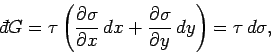 |
(149) |
or
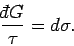 |
(150) |
Thus, dividing the inexact differential
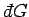 by
by 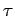 yields the exact
differential
yields the exact
differential 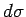 . A factor
. A factor 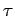 which possesses this property is
termed an integrating factor. Since the above analysis is quite general,
it is clear that an inexact differential involving two independent variables always
admits of an integrating factor. Note, however,
this is not generally the case for inexact
differentials involving more than two variables.
which possesses this property is
termed an integrating factor. Since the above analysis is quite general,
it is clear that an inexact differential involving two independent variables always
admits of an integrating factor. Note, however,
this is not generally the case for inexact
differentials involving more than two variables.
After this mathematical excursion, let us return to physical situation of interest.
The macrostate of a macroscopic system can be specified by the values of the
external parameters (e.g., the volume) and the mean energy  . This, in
turn, fixes other parameters such as the mean pressure
. This, in
turn, fixes other parameters such as the mean pressure 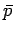 . Alternatively,
we can specify the external parameters and the mean pressure, which fixes the
mean energy. Quantities such as
. Alternatively,
we can specify the external parameters and the mean pressure, which fixes the
mean energy. Quantities such as 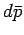 and
and 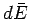 are infinitesimal
differences between well-defined quantities: i.e.,
they are exact differentials.
For example,
are infinitesimal
differences between well-defined quantities: i.e.,
they are exact differentials.
For example,
 is just the difference between the
mean energy of the system in the final macrostate
is just the difference between the
mean energy of the system in the final macrostate 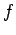 and the
initial macrostate
and the
initial macrostate 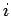 , in the limit where these two states are nearly the same.
It follows that if the system is taken from an initial macrostate
, in the limit where these two states are nearly the same.
It follows that if the system is taken from an initial macrostate 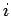 to any
final macrostate
to any
final macrostate 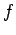 the mean energy change is given by
the mean energy change is given by
 |
(151) |
However, since the mean energy is just a function of the macrostate under consideration, 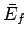 and
and 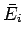 depend only on the initial and final
states, respectively.
Thus, the integral
depend only on the initial and final
states, respectively.
Thus, the integral  depends only on the initial and final
states, and not on the particular process used to get between them.
depends only on the initial and final
states, and not on the particular process used to get between them.
Consider, now, the infinitesimal work done by the system in going from some
initial macrostate 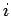 to some neighbouring final macrostate
to some neighbouring final macrostate 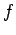 . In general,
. In general,
 is not the difference between two
numbers referring to the properties of two neighbouring macrostates. Instead,
it is merely an infinitesimal quantity characteristic of the process of going
from state
is not the difference between two
numbers referring to the properties of two neighbouring macrostates. Instead,
it is merely an infinitesimal quantity characteristic of the process of going
from state 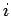 to state
to state 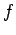 . In other words, the work
. In other words, the work
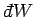 is in general
an inexact differential. The total work done by the system in going from any
macrostate
is in general
an inexact differential. The total work done by the system in going from any
macrostate 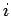 to some other macrostate
to some other macrostate 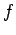 can be written as
can be written as
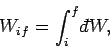 |
(152) |
where the integral represents the sum of the infinitesimal amounts of work
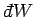 performed at each stage of the process. In general, the value of
the integral does
depend on the particular process used in going from macrostate
performed at each stage of the process. In general, the value of
the integral does
depend on the particular process used in going from macrostate 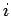 to macrostate
to macrostate 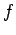 .
.
Recall that in going from macrostate 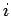 to macrostate
to macrostate 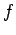 the change
the change
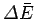 does not
depend on the process used whereas the work
does not
depend on the process used whereas the work  , in general, does.
Thus, it follows from
the first law of thermodynamics, Eq. (123),
that the heat
, in general, does.
Thus, it follows from
the first law of thermodynamics, Eq. (123),
that the heat 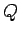 , in general, also depends on the
process used. It follows that
, in general, also depends on the
process used. It follows that
 |
(153) |
is an inexact differential. However, by analogy with the mathematical example
discussed previously, there must exist some integrating factor,  , say, which
converts the inexact differential
, say, which
converts the inexact differential
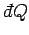 into an exact differential.
So,
into an exact differential.
So,
 |
(154) |
It will be interesting to find out what physical quantities correspond to
the functions  and
and 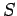 .
.
Suppose that the system is thermally insulated, so that 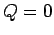 . In this case, the
first law of thermodynamics implies that
. In this case, the
first law of thermodynamics implies that
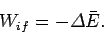 |
(155) |
Thus, in this special case, the work done depends only on the energy
difference between in the initial and final states, and is independent of the process.
In fact, when Clausius first formulated the first law in 1850
this is how he expressed it:
If a thermally isolated system is brought from some initial to some final state
then the work done by the system is independent of the process used.
If the external parameters of the system are kept fixed, so that no work is done,
then
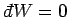 , Eq. (124) reduces
to
, Eq. (124) reduces
to
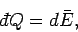 |
(156) |
and
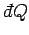 becomes an exact differential. The amount of heat
becomes an exact differential. The amount of heat 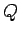 absorbed
in going from one macrostate to another
depends only on the mean energy difference between them, and
is independent of the process used to effect the change. In this situation,
heat is a conserved quantity, and acts very much like the invisible indestructible
fluid of Lavoisier's calorific theory.
absorbed
in going from one macrostate to another
depends only on the mean energy difference between them, and
is independent of the process used to effect the change. In this situation,
heat is a conserved quantity, and acts very much like the invisible indestructible
fluid of Lavoisier's calorific theory.



Next: Statistical thermodynamics
Up: Heat and work
Previous: Quasi-static processes
Richard Fitzpatrick
2006-02-02
![]() is some general
function of two
independent variables
is some general
function of two
independent variables ![]() and
and ![]() . Consider the change in
. Consider the change in ![]() in
going from the point
in
going from the point ![]() ,
, ![]() in the
in the ![]() -
-![]() plane to the neighbouring point
(
plane to the neighbouring point
(![]() ,
, ![]() ). This is given by
). This is given by
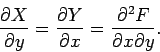
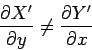
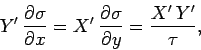
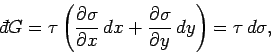
![]() . This, in
turn, fixes other parameters such as the mean pressure
. This, in
turn, fixes other parameters such as the mean pressure ![]() . Alternatively,
we can specify the external parameters and the mean pressure, which fixes the
mean energy. Quantities such as
. Alternatively,
we can specify the external parameters and the mean pressure, which fixes the
mean energy. Quantities such as ![]() and
and ![]() are infinitesimal
differences between well-defined quantities: i.e.,
they are exact differentials.
For example,
are infinitesimal
differences between well-defined quantities: i.e.,
they are exact differentials.
For example,
![]() is just the difference between the
mean energy of the system in the final macrostate
is just the difference between the
mean energy of the system in the final macrostate ![]() and the
initial macrostate
and the
initial macrostate ![]() , in the limit where these two states are nearly the same.
It follows that if the system is taken from an initial macrostate
, in the limit where these two states are nearly the same.
It follows that if the system is taken from an initial macrostate ![]() to any
final macrostate
to any
final macrostate ![]() the mean energy change is given by
the mean energy change is given by
![]() to some neighbouring final macrostate
to some neighbouring final macrostate ![]() . In general,
. In general,
![]() is not the difference between two
numbers referring to the properties of two neighbouring macrostates. Instead,
it is merely an infinitesimal quantity characteristic of the process of going
from state
is not the difference between two
numbers referring to the properties of two neighbouring macrostates. Instead,
it is merely an infinitesimal quantity characteristic of the process of going
from state ![]() to state
to state ![]() . In other words, the work
. In other words, the work
![]() is in general
an inexact differential. The total work done by the system in going from any
macrostate
is in general
an inexact differential. The total work done by the system in going from any
macrostate ![]() to some other macrostate
to some other macrostate ![]() can be written as
can be written as
![]() to macrostate
to macrostate ![]() the change
the change
![]() does not
depend on the process used whereas the work
does not
depend on the process used whereas the work ![]() , in general, does.
Thus, it follows from
the first law of thermodynamics, Eq. (123),
that the heat
, in general, does.
Thus, it follows from
the first law of thermodynamics, Eq. (123),
that the heat ![]() , in general, also depends on the
process used. It follows that
, in general, also depends on the
process used. It follows that
![]() . In this case, the
first law of thermodynamics implies that
. In this case, the
first law of thermodynamics implies that
![]() , Eq. (124) reduces
to
, Eq. (124) reduces
to