

Next: The microscopic interpretation of
Up: Heat and work
Previous: A brief history of
In describing a system made up of a great many particles,
it is usually possible to specify
some macroscopically measurable independent parameters 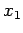 ,
,
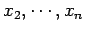 which affect the particles' equations of motion.
These parameters are termed the external parameters the system.
Examples of such parameters are the volume (this gets into the equations
of motion because the potential energy becomes infinite when a particle
strays outside the available volume) and any applied electric and magnetic fields.
A microstate of the system is defined as a state for
which the motions of the individual
particles are completely specified (subject, of course,
to the unavoidable limitations imposed
by the uncertainty principle of quantum mechanics).
In general, the overall energy of a given microstate
which affect the particles' equations of motion.
These parameters are termed the external parameters the system.
Examples of such parameters are the volume (this gets into the equations
of motion because the potential energy becomes infinite when a particle
strays outside the available volume) and any applied electric and magnetic fields.
A microstate of the system is defined as a state for
which the motions of the individual
particles are completely specified (subject, of course,
to the unavoidable limitations imposed
by the uncertainty principle of quantum mechanics).
In general, the overall energy of a given microstate 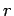 is a function
of the external parameters:
is a function
of the external parameters:
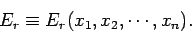 |
(119) |
A macrostate of the system is defined by specifying the external parameters,
and any other constraints to which the system is subject. For example, if we
are dealing with an isolated system (i.e., one that can neither exchange heat with nor
do work on its surroundings) then the macrostate might be specified by giving the
values of the volume and the constant total energy.
For a many-particle system, there are generally a very great
number of microstates which are consistent with a given macrostate.


Next: The microscopic interpretation of
Up: Heat and work
Previous: A brief history of
Richard Fitzpatrick
2006-02-02