


Next: Probability calculations
Up: Statistical mechanics
Previous: The relaxation time
Reversibility and irreversibility
Previously, we mentioned that on a microscopic level the laws of physics are
invariant under time reversal. In other words, microscopic phenomena look
physically plausible when run in reverse. We usually say that these phenomena are
reversible. What about macroscopic phenomena? Are they reversible?
Well, consider an isolated
many particle system which starts off far from equilibrium.
According to the 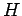 theorem, it will evolve towards
equilibrium and, as it does so, the macroscopic
quantity
theorem, it will evolve towards
equilibrium and, as it does so, the macroscopic
quantity 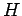 will decrease.
But, if we run this process backwards the system will
appear to evolve away from equilibrium,
and the quantity
will decrease.
But, if we run this process backwards the system will
appear to evolve away from equilibrium,
and the quantity 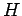 will increase.
This type of behaviour is not physical because it
violates the
will increase.
This type of behaviour is not physical because it
violates the 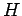 theorem. So, if we saw a film of
a macroscopic process
we could very easily tell if it was being run backwards.
For instance, suppose that by some miracle we were able to move all of the
Oxygen molecules in the air in some classroom to one side of the room, and
all of the Nitrogen molecules to the opposite side. We would not expect this
state to persist for very long. Pretty soon the Oxygen and Nitrogen molecules
would start to intermingle, and this process would
continue until they were thoroughly mixed together throughout the room.
This, of course, is the equilibrium state for air. In reverse, this process
looks crazy! We would start off from perfectly normal air, and
suddenly, for no good reason, the Oxygen and Nitrogen molecules would
appear to separate and move to opposite sides of the room. This scenario
is not impossible, but, from everything we know about the world around us,
it is spectacularly unlikely!
We conclude, therefore, that
macroscopic phenomena are generally irreversible, because they look ``wrong''
when run in reverse.
theorem. So, if we saw a film of
a macroscopic process
we could very easily tell if it was being run backwards.
For instance, suppose that by some miracle we were able to move all of the
Oxygen molecules in the air in some classroom to one side of the room, and
all of the Nitrogen molecules to the opposite side. We would not expect this
state to persist for very long. Pretty soon the Oxygen and Nitrogen molecules
would start to intermingle, and this process would
continue until they were thoroughly mixed together throughout the room.
This, of course, is the equilibrium state for air. In reverse, this process
looks crazy! We would start off from perfectly normal air, and
suddenly, for no good reason, the Oxygen and Nitrogen molecules would
appear to separate and move to opposite sides of the room. This scenario
is not impossible, but, from everything we know about the world around us,
it is spectacularly unlikely!
We conclude, therefore, that
macroscopic phenomena are generally irreversible, because they look ``wrong''
when run in reverse.
How does the irreversibility of macroscopic phenomena arise? It certainly
does not come from the fundamental laws of physics, because these laws
are all reversible.
In the previous example, the Oxygen and Nitrogen molecules got mixed up
by continually scattering off one another. Each individual scattering event
would look perfectly reasonable viewed in reverse, but when we add them all together
we obtain a process which would look stupid run backwards. How can this be?
How can we obtain an irreversible process from the combined effects of
very many reversible
processes? This is a vitally important question. Unfortunately, we are not
quite at the stage where we can formulate a convincing answer. Note, however, that the essential irreversibility of macroscopic phenomena is one of the
key results of statistical thermodynamics.



Next: Probability calculations
Up: Statistical mechanics
Previous: The relaxation time
Richard Fitzpatrick
2006-02-02