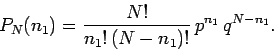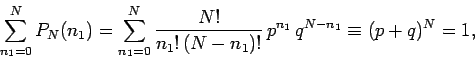Next: The mean, variance, and
Up: Probability theory
Previous: Combinatorial analysis
It follows from Eqs. (16) and (20) that the probability of obtaining
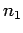 occurrences of the
outcome 1 in
occurrences of the
outcome 1 in  statistically independent observations of a two-state system
is
statistically independent observations of a two-state system
is
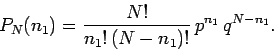 |
(21) |
This probability function is called the binomial distribution function.
The reason for this is obvious if we tabulate the probabilities for the
first few possible values of  (see Tab. 1).
(see Tab. 1).
Table 1:
The binomial probability distribution
|
|
Of course, we immediately recognize these expressions:
they appear in the standard
algebraic expansions of 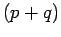 ,
, 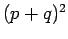 ,
, 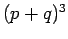 , and
, and 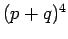 ,
respectively. In algebra, the expansion of
,
respectively. In algebra, the expansion of  is called the
binomial expansion (hence, the name given to the probability distribution
function),
and can be written
is called the
binomial expansion (hence, the name given to the probability distribution
function),
and can be written
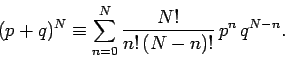 |
(22) |
Equations (21) and (22) can be used to establish the normalization
condition for the binomial distribution function:
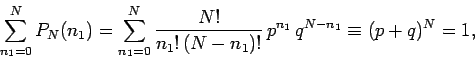 |
(23) |
since  .
.



Next: The mean, variance, and
Up: Probability theory
Previous: Combinatorial analysis
Richard Fitzpatrick
2006-02-02