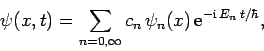Next: Square Potential Barrier
Up: One-Dimensional Potentials
Previous: Introduction
Infinite Potential Well
Consider a particle of mass 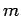 and energy
and energy 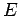 moving in the following simple potential:
moving in the following simple potential:
![\begin{displaymath}
V(x) = \left\{\begin{array}{lcl}
0&\mbox{\hspace{1cm}}&\mbox...
...leq a$}\ [0.5ex]
\infty&&\mbox{otherwise}
\end{array}\right..
\end{displaymath}](img788.png) |
(302) |
It follows from Eq. (301) that if 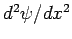 (and, hence,
(and, hence,  ) is
to remain finite then
) is
to remain finite then  must go to zero in regions where the potential
is infinite. Hence,
must go to zero in regions where the potential
is infinite. Hence, 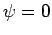 in the regions
in the regions 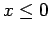 and
and  .
Evidently, the problem is equivalent to that of a particle trapped in a
one-dimensional box of length
.
Evidently, the problem is equivalent to that of a particle trapped in a
one-dimensional box of length 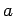 .
The boundary conditions on
.
The boundary conditions on  in
the region
in
the region 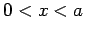 are
are
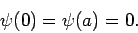 |
(303) |
Furthermore, it follows from Eq. (301) that  satisfies
satisfies
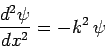 |
(304) |
in this region, where
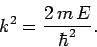 |
(305) |
Here, we are assuming that  . It is easily demonstrated that there are
no solutions with
. It is easily demonstrated that there are
no solutions with  which are capable of satisfying the boundary conditions (303).
which are capable of satisfying the boundary conditions (303).
The solution to Eq. (304), subject to the boundary conditions
(303), is
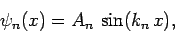 |
(306) |
where the 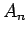 are arbitrary (real) constants, and
are arbitrary (real) constants, and
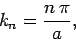 |
(307) |
for
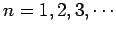 . Now, it can be seen from Eqs. (305) and (307)
that the energy
. Now, it can be seen from Eqs. (305) and (307)
that the energy 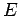 is only allowed to take certain discrete values:
i.e.,
is only allowed to take certain discrete values:
i.e.,
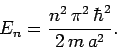 |
(308) |
In other words, the eigenvalues of the energy operator are discrete. This
is a general feature of bounded solutions: i.e., solutions in which
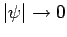 as
as
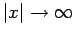 . According to the discussion in Sect. 4.12,
we expect the stationary eigenfunctions
. According to the discussion in Sect. 4.12,
we expect the stationary eigenfunctions 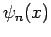 to satisfy
the orthonormality constraint
to satisfy
the orthonormality constraint
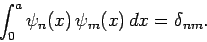 |
(309) |
It is easily demonstrated that this is the case, provided
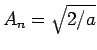 .
Hence,
.
Hence,
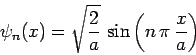 |
(310) |
for
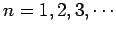 .
.
Finally, again from Sect. 4.12, the general time-dependent solution can be written as a linear superposition of stationary solutions:
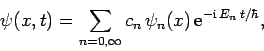 |
(311) |
where
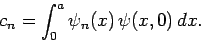 |
(312) |



Next: Square Potential Barrier
Up: One-Dimensional Potentials
Previous: Introduction
Richard Fitzpatrick
2010-07-20
![\begin{displaymath}
V(x) = \left\{\begin{array}{lcl}
0&\mbox{\hspace{1cm}}&\mbox...
...leq a$}\ [0.5ex]
\infty&&\mbox{otherwise}
\end{array}\right..
\end{displaymath}](img788.png)
![\begin{displaymath}
V(x) = \left\{\begin{array}{lcl}
0&\mbox{\hspace{1cm}}&\mbox...
...leq a$}\ [0.5ex]
\infty&&\mbox{otherwise}
\end{array}\right..
\end{displaymath}](img788.png)
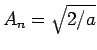 .
Hence,
.
Hence,