


Next: One-Dimensional Potentials
Up: Stationary States
Previous: Stationary States
- Monochromatic light with a wavelength of
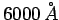 passes
through a fast shutter that opens for
passes
through a fast shutter that opens for 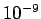 sec. What is the
subsequent spread in wavelengths of the no longer monochromatic light?
sec. What is the
subsequent spread in wavelengths of the no longer monochromatic light?
- Calculate
 ,
,
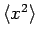 , and
, and 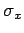 , as
well as
, as
well as
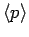 ,
,
 , and
, and 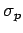 ,
for the normalized wavefunction
,
for the normalized wavefunction
Use these to find
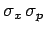 . Note that
. Note that
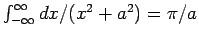 .
.
- Classically, if a particle is not observed then the probability of finding it
in a one-dimensional box of length
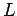 , which extends from
, which extends from 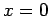 to
to  , is a constant
, is a constant 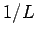 per unit length.
Show that the classical expectation value of
per unit length.
Show that the classical expectation value of  is
is 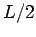 , the expectation value of
, the expectation value of
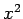 is
is 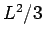 , and the standard deviation of
, and the standard deviation of  is
is 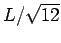 .
.
- Demonstrate that if a particle in a one-dimensional stationary state is bound then the
expectation value of its momentum must be zero.
- Suppose that
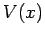 is complex. Obtain an expression for
is complex. Obtain an expression for
 and
and
 from Schrödinger's equation. What does this tell us about a complex
from Schrödinger's equation. What does this tell us about a complex 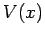 ?
?
 and
and 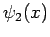 are normalized eigenfunctions corresponding to
the same eigenvalue. If
are normalized eigenfunctions corresponding to
the same eigenvalue. If
where 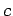 is real, find normalized linear combinations of
is real, find normalized linear combinations of  and
and
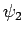 which are orthogonal to (a)
which are orthogonal to (a)  , (b)
, (b) 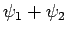 .
.
- Demonstrate that
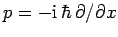 is an Hermitian
operator. Find the Hermitian conjugate of
is an Hermitian
operator. Find the Hermitian conjugate of
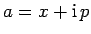 .
.
- An operator
 , corresponding to a physical quantity
, corresponding to a physical quantity 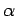 , has
two normalized eigenfunctions
, has
two normalized eigenfunctions  and
and 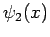 , with eigenvalues
, with eigenvalues
 and
and 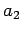 . An operator
. An operator  , corresponding to another physical
quantity
, corresponding to another physical
quantity 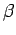 , has normalized eigenfunctions
, has normalized eigenfunctions 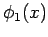 and
and 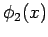 ,
with eigenvalues
,
with eigenvalues 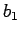 and
and 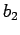 . The eigenfunctions are
related via
. The eigenfunctions are
related via
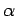 is measured and the value
is measured and the value  is obtained. If
is obtained. If 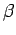 is then measured and then
is then measured and then 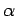 again, show that the probability of obtaining
again, show that the probability of obtaining
 a second time is
a second time is  .
.
- Demonstrate that an operator which commutes with the
Hamiltonian, and contains no explicit time dependence, has an expectation
value which is constant in time.
- For a certain system, the operator corresponding to the physical
quantity
 does not commute with the Hamiltonian. It has
eigenvalues
does not commute with the Hamiltonian. It has
eigenvalues  and
and 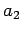 , corresponding to properly normalized eigenfunctions
, corresponding to properly normalized eigenfunctions
where 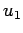 and
and 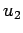 are properly normalized eigenfunctions of the
Hamiltonian with eigenvalues
are properly normalized eigenfunctions of the
Hamiltonian with eigenvalues  and
and 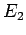 . If the system is in the
state
. If the system is in the
state 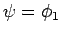 at time
at time 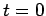 , show that the expectation value of
, show that the expectation value of  at time
at time  is
is



Next: One-Dimensional Potentials
Up: Stationary States
Previous: Stationary States
Richard Fitzpatrick
2010-07-20
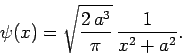
![\begin{displaymath}
\langle A\rangle = \left(\frac{a_1+a_2}{2}\right) + \left(\f...
...a_1-a_2}{2}\right)\cos\left(\frac{[E_1-E_2] t}{\hbar}\right).
\end{displaymath}](img785.png)
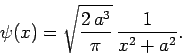
![\begin{displaymath}
\langle A\rangle = \left(\frac{a_1+a_2}{2}\right) + \left(\f...
...a_1-a_2}{2}\right)\cos\left(\frac{[E_1-E_2] t}{\hbar}\right).
\end{displaymath}](img785.png)