


Next: Collapse of the Wave
Up: Wave-Particle Duality
Previous: Heisenberg's Uncertainty Principle
Schrödinger's Equation
We have seen that the wavefunction of a free particle of mass 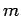 satisfies
satisfies
 |
(128) |
where 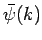 is determined by
is determined by 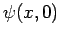 , and
, and
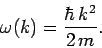 |
(129) |
Now, it follows from Eq. (128) that
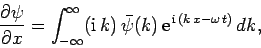 |
(130) |
and
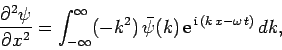 |
(131) |
whereas
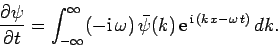 |
(132) |
Thus,
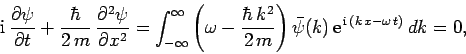 |
(133) |
where use has been made of the dispersion relation (129).
Multiplying through by 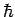 , we obtain
, we obtain
 |
(134) |
This expression is known as Schrödinger's equation, since it was first
introduced by Erwin Schrödinger in 1925. Schrödinger's equation
is a linear, second-order, partial differential equation which governs the time evolution of a particle
wavefunction, and is generally easier to solve than the integral equation
(128).
Of course, Eq. (134) is only applicable to freely
moving particles. Fortunately, it is fairly easy to guess the generalization of this
equation for particles moving in some potential 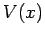 . It is plausible, from Eq. (130), that we can identify
. It is plausible, from Eq. (130), that we can identify
 with the differential operator
with the differential operator
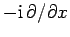 .
Hence, the differential operator on the right-hand side of Eq. (134)
is equivalent to
.
Hence, the differential operator on the right-hand side of Eq. (134)
is equivalent to
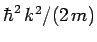 . But,
. But, 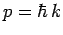 . Thus,
the operator is also equivalent to
. Thus,
the operator is also equivalent to  , which is just the energy of
a freely moving particle. However, in the presence of a potential
, which is just the energy of
a freely moving particle. However, in the presence of a potential
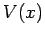 , the particle's energy is written
, the particle's energy is written
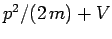 . Thus, it
seems reasonable to make the substitution
. Thus, it
seems reasonable to make the substitution
 |
(135) |
This leads to the general form of Schrödinger's equation:
 |
(136) |



Next: Collapse of the Wave
Up: Wave-Particle Duality
Previous: Heisenberg's Uncertainty Principle
Richard Fitzpatrick
2010-07-20
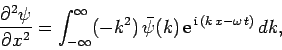
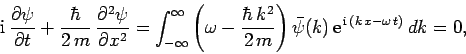
![]() . It is plausible, from Eq. (130), that we can identify
. It is plausible, from Eq. (130), that we can identify
![]() with the differential operator
with the differential operator
![]() .
Hence, the differential operator on the right-hand side of Eq. (134)
is equivalent to
.
Hence, the differential operator on the right-hand side of Eq. (134)
is equivalent to
![]() . But,
. But, ![]() . Thus,
the operator is also equivalent to
. Thus,
the operator is also equivalent to ![]() , which is just the energy of
a freely moving particle. However, in the presence of a potential
, which is just the energy of
a freely moving particle. However, in the presence of a potential
![]() , the particle's energy is written
, the particle's energy is written
![]() . Thus, it
seems reasonable to make the substitution
. Thus, it
seems reasonable to make the substitution