

Next: Classical Light Waves
Up: Wave-Particle Duality
Previous: Plane Waves
In mathematics, the symbol 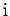 is conventionally used to represent the square-root of minus one: i.e., one of the
solutions of
is conventionally used to represent the square-root of minus one: i.e., one of the
solutions of
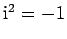 . Now, a real number,
. Now, a real number,  (say), can take any value in a continuum of different values lying between
(say), can take any value in a continuum of different values lying between 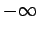 and
and 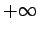 .
On the other hand, an imaginary number takes the general form
.
On the other hand, an imaginary number takes the general form 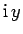 , where
, where 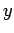 is a real number. It follows that the square of
a real number is a positive real number, whereas the square of an imaginary number is a negative real number. In addition, a general complex number is written
is a real number. It follows that the square of
a real number is a positive real number, whereas the square of an imaginary number is a negative real number. In addition, a general complex number is written
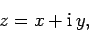 |
(36) |
where  and
and 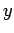 are real numbers. In fact,
are real numbers. In fact,  is termed the real part of
is termed the real part of 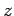 , and
, and 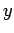 the imaginary part of
the imaginary part of 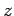 . This is written mathematically as
. This is written mathematically as 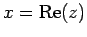 and
and 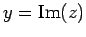 .
Finally, the complex conjugate of
.
Finally, the complex conjugate of 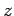 is defined
is defined
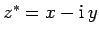 .
.
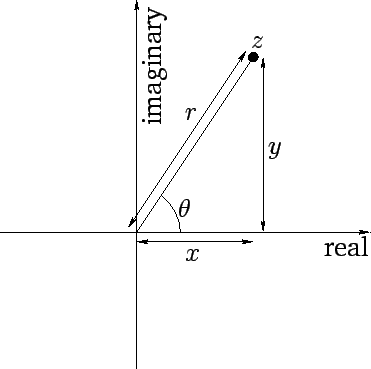
Now, just as we
can visualize a real number as a point on an infinite straight-line, we can visualize a complex number as
a point in an infinite plane. The coordinates of the point in question are the real and imaginary
parts of the number: i.e.,
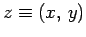 . This idea is illustrated in Fig. 3.
The distance,
. This idea is illustrated in Fig. 3.
The distance,
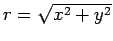 , of the representative point from the origin is termed the modulus
of the corresponding complex number,
, of the representative point from the origin is termed the modulus
of the corresponding complex number, 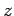 . This is written mathematically as
. This is written mathematically as
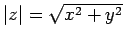 . Incidentally, it follows that
. Incidentally, it follows that
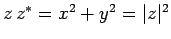 .
The angle,
.
The angle,
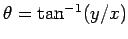 , that the straight-line joining the representative point to the origin subtends with the
real axis is termed the argument of the corresponding complex number,
, that the straight-line joining the representative point to the origin subtends with the
real axis is termed the argument of the corresponding complex number, 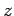 . This is written mathematically
as
. This is written mathematically
as
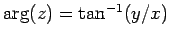 . It follows from standard trigonometry that
. It follows from standard trigonometry that
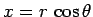 , and
, and
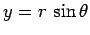 .
Hence,
.
Hence,
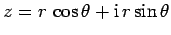 .
.
Figure 3:
Representation of a complex number as a point in a plane.
 |
Complex numbers are often used to represent wavefunctions. All such representations depend ultimately on a fundamental mathematical identity, known as
de Moivre's theorem, which takes the form
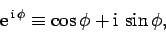 |
(37) |
where 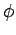 is a real number. Incidentally, given that
is a real number. Incidentally, given that
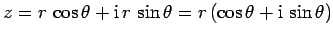 , where
, where 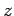 is a general
complex number,
is a general
complex number, 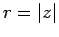 its modulus, and
its modulus, and
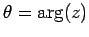 its argument, it follows from de Moivre's theorem that any
complex number,
its argument, it follows from de Moivre's theorem that any
complex number, 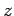 , can be written
, can be written
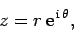 |
(38) |
where 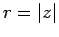 and
and
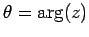 are real numbers.
are real numbers.
Now, a one-dimensional wavefunction takes the general form
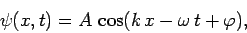 |
(39) |
where 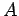 is the wave amplitude,
is the wave amplitude, 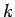 the wavenumber,
the wavenumber, 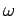 the angular
frequency, and
the angular
frequency, and 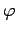 the phase angle. Consider the complex wavefunction
the phase angle. Consider the complex wavefunction
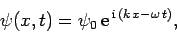 |
(40) |
where 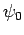 is a complex constant. We can write
is a complex constant. We can write
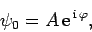 |
(41) |
where 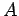 is the modulus, and
is the modulus, and 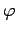 the argument, of
the argument, of 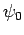 .
Hence, we deduce that
.
Hence, we deduce that
Thus, it follows from de Moirve's theorem, and Eq. (39), that
![\begin{displaymath}
{\rm Re}\left[\psi_0 {\rm e}^{ {\rm i} (k x-\omega t)}\right] =A \cos(k x-\omega t+\varphi)=\psi(x,t).
\end{displaymath}](img224.png) |
(43) |
In other words, a general one-dimensional real wavefunction, (39), can be
represented as the real part of a complex wavefunction of the form (40).
For ease
of notation, the ``take the real part'' aspect of the above expression is usually omitted, and our general one-dimension wavefunction
is simply written
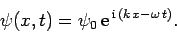 |
(44) |
The
main advantage of the complex representation, (44), over the more straightforward
real representation, (39), is that the former enables us to combine the amplitude, 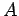 , and the
phase angle,
, and the
phase angle, 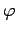 , of the wavefunction into a single complex amplitude,
, of the wavefunction into a single complex amplitude, 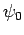 .
Finally, the three dimensional generalization of the above expression is
.
Finally, the three dimensional generalization of the above expression is
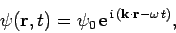 |
(45) |
where 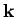 is the wavevector.
is the wavevector.


Next: Classical Light Waves
Up: Wave-Particle Duality
Previous: Plane Waves
Richard Fitzpatrick
2010-07-20
![]() . This idea is illustrated in Fig. 3.
The distance,
. This idea is illustrated in Fig. 3.
The distance,
![]() , of the representative point from the origin is termed the modulus
of the corresponding complex number,
, of the representative point from the origin is termed the modulus
of the corresponding complex number, ![]() . This is written mathematically as
. This is written mathematically as
![]() . Incidentally, it follows that
. Incidentally, it follows that
![]() .
The angle,
.
The angle,
![]() , that the straight-line joining the representative point to the origin subtends with the
real axis is termed the argument of the corresponding complex number,
, that the straight-line joining the representative point to the origin subtends with the
real axis is termed the argument of the corresponding complex number, ![]() . This is written mathematically
as
. This is written mathematically
as
![]() . It follows from standard trigonometry that
. It follows from standard trigonometry that
![]() , and
, and
![]() .
Hence,
.
Hence,
![]() .
.