


Next: General Principles
Up: Addition of Angular Momentum
Previous: Addition of Angular Momentum
Consider an electron in a hydrogen atom. As we have already seen, the electron's motion through space is parameterized by the three quantum numbers  ,
, 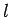 ,
and
,
and  (see Sect. 9.4). To these we must now add the
two quantum numbers
(see Sect. 9.4). To these we must now add the
two quantum numbers 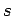 and
and 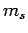 which parameterize the electron's internal
motion (see the previous chapter). Now, the quantum numbers
which parameterize the electron's internal
motion (see the previous chapter). Now, the quantum numbers 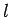 and
and  specify the electron's orbital angular momentum vector,
specify the electron's orbital angular momentum vector,  , (as much as it can be specified) whereas
the quantum numbers
, (as much as it can be specified) whereas
the quantum numbers 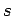 and
and 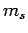 specify its spin angular momentum vector,
specify its spin angular momentum vector,
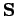 . But, if the electron possesses both orbital
and spin angular momentum then what is its total angular momentum?
. But, if the electron possesses both orbital
and spin angular momentum then what is its total angular momentum?
Richard Fitzpatrick
2010-07-20