


Next: Eigenstates of and
Up: Spin Angular Momentum
Previous: Spin Operators
Spin Space
We now have to discuss the wavefunctions upon which the previously introduced
spin operators act. Unlike regular wavefunctions, spin wavefunctions
do not exist in real space. Likewise, the spin angular momentum operators
cannot be represented as differential operators in real space.
Instead, we need to think of spin wavefunctions as
existing in an abstract (complex) vector space. The different members of
this space correspond to the different internal configurations of the particle
under investigation.
Note that only the directions of our vectors have any physical significance
(just as only the shape of a regular wavefunction has any physical
significance). Thus,
if the vector 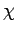 corresponds to a particular internal state then
corresponds to a particular internal state then
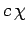 corresponds to the same state, where
corresponds to the same state, where  is a complex number.
Now, we expect the internal states of our particle to be superposable,
since the superposability of states is one of the fundamental assumptions of
quantum mechanics.
It follows that the vectors making up our vector space must also be superposable.
Thus, if
is a complex number.
Now, we expect the internal states of our particle to be superposable,
since the superposability of states is one of the fundamental assumptions of
quantum mechanics.
It follows that the vectors making up our vector space must also be superposable.
Thus, if 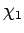 and
and 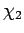 are two vectors corresponding to two
different internal states then
are two vectors corresponding to two
different internal states then
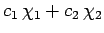 is another vector
corresponding to the state obtained by superposing
is another vector
corresponding to the state obtained by superposing  times state 1
with
times state 1
with 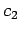 times state 2 (where
times state 2 (where  and
and 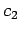 are complex numbers). Finally, the dimensionality of our vector
space is simply the number of linearly independent vectors required to span
it (i.e., the number of linearly independent internal states of the
particle under investigation).
are complex numbers). Finally, the dimensionality of our vector
space is simply the number of linearly independent vectors required to span
it (i.e., the number of linearly independent internal states of the
particle under investigation).
We now need to define the length of our vectors. We can do this by
introducing a second, or dual, vector space whose elements are in one to one
correspondence with the elements of our first space. Let the element of the second
space which corresponds to the element 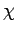 of the first space
be called
of the first space
be called  . Moreover, the element of the second space
which corresponds to
. Moreover, the element of the second space
which corresponds to 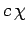 is
is
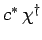 . We shall assume
that it is possible to combine
. We shall assume
that it is possible to combine 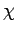 and
and  in a multiplicative
fashion to generate a real
positive-definite number which we interpret as the length, or norm,
of
in a multiplicative
fashion to generate a real
positive-definite number which we interpret as the length, or norm,
of 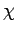 . Let us denote this number
. Let us denote this number
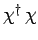 . Thus, we
have
. Thus, we
have
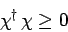 |
(713) |
for all 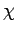 . We shall also assume that it is possible to combine unlike states
in an analogous multiplicative fashion to produce complex numbers. The
product of two unlike states
. We shall also assume that it is possible to combine unlike states
in an analogous multiplicative fashion to produce complex numbers. The
product of two unlike states 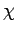 and
and  is denoted
is denoted
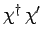 .
Two states
.
Two states 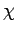 and
and  are said to be mutually orthogonal, or independent,
if
are said to be mutually orthogonal, or independent,
if
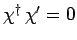 .
.
Now, when a general spin operator, 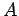 , operates on a general spin-state,
, operates on a general spin-state, 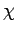 , it coverts it into a different spin-state which we shall denote
, it coverts it into a different spin-state which we shall denote
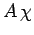 . The dual of this state is
. The dual of this state is
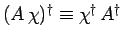 , where
, where 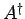 is the Hermitian conjugate of
is the Hermitian conjugate of 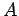 (this is the definition of an
Hermitian conjugate in spin space). An eigenstate
of
(this is the definition of an
Hermitian conjugate in spin space). An eigenstate
of 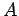 corresponding to the eigenvalue
corresponding to the eigenvalue 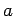 satisfies
satisfies
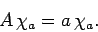 |
(714) |
As before, if 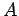 corresponds to a physical variable then a measurement
of
corresponds to a physical variable then a measurement
of 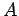 will result in one of its eigenvalues (see Sect. 4.10). In order to ensure that
these eigenvalues are all real,
will result in one of its eigenvalues (see Sect. 4.10). In order to ensure that
these eigenvalues are all real, 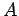 must be Hermitian: i.e.,
must be Hermitian: i.e.,  (see Sect. 4.9). We expect the
(see Sect. 4.9). We expect the 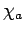 to be mutually orthogonal. We
can also normalize them such that they all have unit length. In other words,
to be mutually orthogonal. We
can also normalize them such that they all have unit length. In other words,
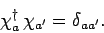 |
(715) |
Finally, a general spin state can be written
as a superposition of the normalized eigenstates of 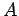 : i.e.,
: i.e.,
 |
(716) |
A measurement of 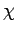 will then yield the result
will then yield the result 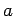 with probability
with probability 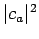 .
.



Next: Eigenstates of and
Up: Spin Angular Momentum
Previous: Spin Operators
Richard Fitzpatrick
2010-07-20
![]() of the first space
be called
of the first space
be called ![]() . Moreover, the element of the second space
which corresponds to
. Moreover, the element of the second space
which corresponds to ![]() is
is
![]() . We shall assume
that it is possible to combine
. We shall assume
that it is possible to combine ![]() and
and ![]() in a multiplicative
fashion to generate a real
positive-definite number which we interpret as the length, or norm,
of
in a multiplicative
fashion to generate a real
positive-definite number which we interpret as the length, or norm,
of ![]() . Let us denote this number
. Let us denote this number
![]() . Thus, we
have
. Thus, we
have
![]() , operates on a general spin-state,
, operates on a general spin-state, ![]() , it coverts it into a different spin-state which we shall denote
, it coverts it into a different spin-state which we shall denote
![]() . The dual of this state is
. The dual of this state is
![]() , where
, where ![]() is the Hermitian conjugate of
is the Hermitian conjugate of ![]() (this is the definition of an
Hermitian conjugate in spin space). An eigenstate
of
(this is the definition of an
Hermitian conjugate in spin space). An eigenstate
of ![]() corresponding to the eigenvalue
corresponding to the eigenvalue ![]() satisfies
satisfies