


Next: Three-Dimensional Quantum Mechanics
Up: Identical Particles
Previous: Identical Particles
- Consider a system consisting of two non-interacting particles, and three
one-particle states,
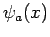 ,
, 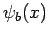 , and
, and 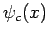 . How
many different two-particle states can be constructed if the particles are
(a) distinguishable, (b) indistinguishable bosons, or (c) indistinguishable
fermions?
. How
many different two-particle states can be constructed if the particles are
(a) distinguishable, (b) indistinguishable bosons, or (c) indistinguishable
fermions?
- Consider two non-interacting particles, each of mass
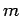 , in
a one-dimensional harmonic oscillator potential of classical oscillation
frequency
, in
a one-dimensional harmonic oscillator potential of classical oscillation
frequency 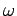 . If one particle is in the ground-state, and the
other in the first excited state, calculate
. If one particle is in the ground-state, and the
other in the first excited state, calculate
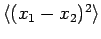 assuming that the particles are (a) distinguishable, (b) indistinguishable bosons, or (c) indistinguishable fermions.
assuming that the particles are (a) distinguishable, (b) indistinguishable bosons, or (c) indistinguishable fermions.
- Two non-interacting particles, with the same mass
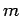 , are
in a one-dimensional box of length
, are
in a one-dimensional box of length 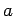 . What are the four lowest
energies of the system? What are the degeneracies of these
energies if the two particles are (a) distinguishable, (b) indistinguishable
bosons, or (c) indistingishable fermions?
. What are the four lowest
energies of the system? What are the degeneracies of these
energies if the two particles are (a) distinguishable, (b) indistinguishable
bosons, or (c) indistingishable fermions?
- Two particles in a one-dimensional box of length
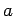 occupy
the
occupy
the 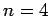 and
and 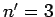 states. Write the properly normalized
wavefunctions if the particles are (a) distinguishable, (b) indistinguishable
bosons, or (c) indistinguishable fermions.
states. Write the properly normalized
wavefunctions if the particles are (a) distinguishable, (b) indistinguishable
bosons, or (c) indistinguishable fermions.



Next: Three-Dimensional Quantum Mechanics
Up: Identical Particles
Previous: Identical Particles
Richard Fitzpatrick
2010-07-20