


Next: Square Potential Well
Up: One-Dimensional Potentials
Previous: Cold Emission
Many types of heavy atomic nucleus spontaneously decay to produce daughter nucleii
via the emission of  -particles (i.e., helium nucleii) of some characteristic energy.
This process is know as
-particles (i.e., helium nucleii) of some characteristic energy.
This process is know as
 -decay. Let us investigate the
-decay. Let us investigate the  -decay of a particular type of atomic nucleus of radius
-decay of a particular type of atomic nucleus of radius 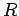 , charge-number
, charge-number 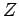 ,
and mass-number
,
and mass-number 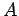 . Such a nucleus thus decays to produce a daughter
nucleus of charge-number
. Such a nucleus thus decays to produce a daughter
nucleus of charge-number  and mass-number
and mass-number 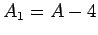 ,
and an
,
and an  -particle of charge-number
-particle of charge-number 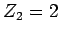 and mass-number
and mass-number
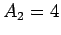 . Let the characteristic energy of the
. Let the characteristic energy of the  -particle
be
-particle
be 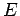 . Incidentally, nuclear radii
are found to satisfy the empirical formula
. Incidentally, nuclear radii
are found to satisfy the empirical formula
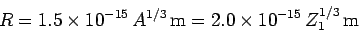 |
(353) |
for 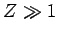 .
.
In 1928, George Gamov proposed a very successful theory of  -decay,
according to which the
-decay,
according to which the  -particle moves freely inside the nucleus, and is emitted after tunneling through the
potential barrier between itself and the daughter nucleus. In other words,
the
-particle moves freely inside the nucleus, and is emitted after tunneling through the
potential barrier between itself and the daughter nucleus. In other words,
the  -particle, whose energy is
-particle, whose energy is 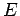 , is trapped in a potential well of radius
, is trapped in a potential well of radius 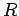 by the
potential barrier
by the
potential barrier
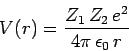 |
(354) |
for 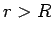 .
.
Making use of the WKB approximation (and neglecting the fact
that 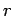 is a radial, rather than a Cartesian, coordinate), the probability
of the
is a radial, rather than a Cartesian, coordinate), the probability
of the  -particle tunneling through the barrier is
-particle tunneling through the barrier is
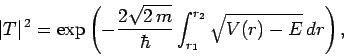 |
(355) |
where 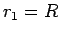 and
and
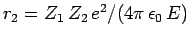 . Here,
. Here,
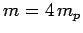 is the
is the  -particle mass. The above expression
reduces to
-particle mass. The above expression
reduces to
![\begin{displaymath}
\vert T\vert^{ 2} = \exp\left(-2 \sqrt{2} \beta \int_{1}^{E_c/E}\left[\frac{1}{y}-\frac{E}{E_c}\right]^{1/2} dy\right),
\end{displaymath}](img921.png) |
(356) |
where
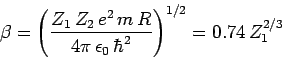 |
(357) |
is a dimensionless constant, and
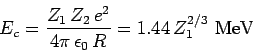 |
(358) |
is the characteristic energy the  -particle would need in order to escape
from the nucleus without tunneling. Of course,
-particle would need in order to escape
from the nucleus without tunneling. Of course,  .
It is easily demonstrated that
.
It is easily demonstrated that
![\begin{displaymath}
\int_1^{1/\epsilon}\left[\frac{1}{y} - \epsilon\right]^{1/2} dy \simeq
\frac{\pi}{2 \sqrt{\epsilon}}-2
\end{displaymath}](img925.png) |
(359) |
when 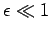 .
Hence.
.
Hence.
![\begin{displaymath}
\vert T\vert^{ 2} \simeq \exp\left(-2 \sqrt{2} \beta\left[\frac{\pi}{2}\sqrt{\frac{E_c}{E}}-2\right]\right).
\end{displaymath}](img927.png) |
(360) |
Now, the  -particle moves inside the nucleus with the characteristic
velocity
-particle moves inside the nucleus with the characteristic
velocity
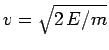 . It follows that the particle bounces backward
and forward within the nucleus at the frequency
. It follows that the particle bounces backward
and forward within the nucleus at the frequency
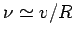 , giving
, giving
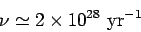 |
(361) |
for a 1 MeV  -particle trapped inside a typical heavy nucleus of radius
-particle trapped inside a typical heavy nucleus of radius 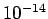 m.
Thus, the
m.
Thus, the  -particle effectively attempts to tunnel through the potential
barrier
-particle effectively attempts to tunnel through the potential
barrier 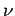 times a second. If each of these attempts has a probability
times a second. If each of these attempts has a probability
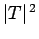 of succeeding, then the probability of decay per unit time
is
of succeeding, then the probability of decay per unit time
is 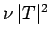 . Hence, if there are
. Hence, if there are  undecayed nuclii at time
undecayed nuclii at time  then
there are only
then
there are only 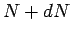 at time
at time 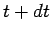 , where
, where
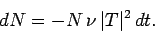 |
(362) |
This expression can be integrated to give
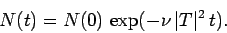 |
(363) |
Now, the half-life,  , is defined as the time which must elapse
in order for half of the nuclii originally present to decay. It follows from
the above formula that
, is defined as the time which must elapse
in order for half of the nuclii originally present to decay. It follows from
the above formula that
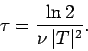 |
(364) |
Note that the half-life is independent of 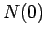 .
.
Finally, making use of the above results, we obtain
![\begin{displaymath}
\log_{10}[\tau ({\rm yr})] = -C_1 - C_2 Z_1^{ 2/3} + C_3 \frac{Z_1}{\sqrt{E({\rm MeV})}},
\end{displaymath}](img940.png) |
(365) |
where
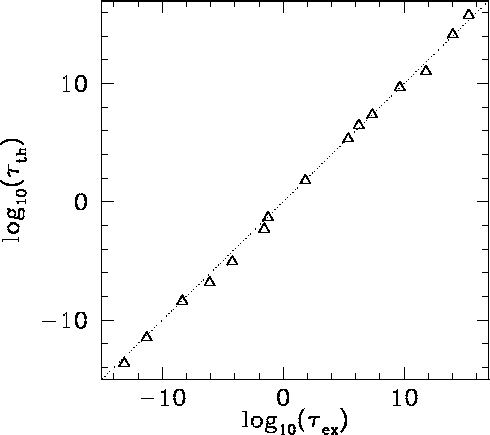
Figure 15:
The experimentally determined half-life, 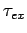 , of various atomic nucleii which decay via
, of various atomic nucleii which decay via  emission versus the best-fit theoretical half-life
emission versus the best-fit theoretical half-life
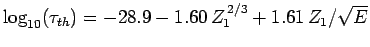 . Both half-lives are measured in years. Here,
. Both half-lives are measured in years. Here,  , where
, where 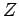 is the charge number of the nucleus, and
is the charge number of the nucleus, and 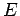 the characteristic energy of the emitted
the characteristic energy of the emitted  -particle in MeV. In
order of increasing half-life, the points correspond to the
following nucleii: Rn 215, Po 214, Po 216, Po 197, Fm 250, Ac 225, U 230, U 232, U 234, Gd 150, U 236, U 238, Pt 190, Gd 152, Nd 144. Data obtained from IAEA Nuclear Data Centre.
-particle in MeV. In
order of increasing half-life, the points correspond to the
following nucleii: Rn 215, Po 214, Po 216, Po 197, Fm 250, Ac 225, U 230, U 232, U 234, Gd 150, U 236, U 238, Pt 190, Gd 152, Nd 144. Data obtained from IAEA Nuclear Data Centre.
 |
The half-life,  , the daughter charge-number,
, the daughter charge-number,  , and
the
, and
the  -particle energy,
-particle energy, 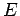 , for atomic nucleii which undergo
, for atomic nucleii which undergo  -decay
are indeed found to satisfy a relationship of the form (365). The
best fit to the data (see Fig. 15) is obtained using
-decay
are indeed found to satisfy a relationship of the form (365). The
best fit to the data (see Fig. 15) is obtained using
Note that these values are remarkably similar to those calculated above.



Next: Square Potential Well
Up: One-Dimensional Potentials
Previous: Cold Emission
Richard Fitzpatrick
2010-07-20
![]() -decay,
according to which the
-decay,
according to which the ![]() -particle moves freely inside the nucleus, and is emitted after tunneling through the
potential barrier between itself and the daughter nucleus. In other words,
the
-particle moves freely inside the nucleus, and is emitted after tunneling through the
potential barrier between itself and the daughter nucleus. In other words,
the ![]() -particle, whose energy is
-particle, whose energy is ![]() , is trapped in a potential well of radius
, is trapped in a potential well of radius ![]() by the
potential barrier
by the
potential barrier
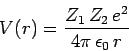
![]() is a radial, rather than a Cartesian, coordinate), the probability
of the
is a radial, rather than a Cartesian, coordinate), the probability
of the ![]() -particle tunneling through the barrier is
-particle tunneling through the barrier is
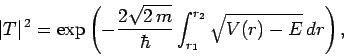
![\begin{displaymath}
\vert T\vert^{ 2} = \exp\left(-2 \sqrt{2} \beta \int_{1}^{E_c/E}\left[\frac{1}{y}-\frac{E}{E_c}\right]^{1/2} dy\right),
\end{displaymath}](img921.png)
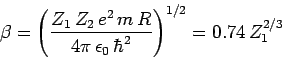
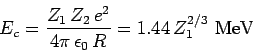
![\begin{displaymath}
\int_1^{1/\epsilon}\left[\frac{1}{y} - \epsilon\right]^{1/2} dy \simeq
\frac{\pi}{2 \sqrt{\epsilon}}-2
\end{displaymath}](img925.png)
![\begin{displaymath}
\vert T\vert^{ 2} \simeq \exp\left(-2 \sqrt{2} \beta\left[\frac{\pi}{2}\sqrt{\frac{E_c}{E}}-2\right]\right).
\end{displaymath}](img927.png)
![]() -particle moves inside the nucleus with the characteristic
velocity
-particle moves inside the nucleus with the characteristic
velocity
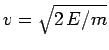 . It follows that the particle bounces backward
and forward within the nucleus at the frequency
. It follows that the particle bounces backward
and forward within the nucleus at the frequency
![]() , giving
, giving
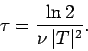

![]() , the daughter charge-number,
, the daughter charge-number, ![]() , and
the
, and
the ![]() -particle energy,
-particle energy, ![]() , for atomic nucleii which undergo
, for atomic nucleii which undergo ![]() -decay
are indeed found to satisfy a relationship of the form (365). The
best fit to the data (see Fig. 15) is obtained using
-decay
are indeed found to satisfy a relationship of the form (365). The
best fit to the data (see Fig. 15) is obtained using