


Next: Heisenberg's Uncertainty Principle
Up: Wave-Particle Duality
Previous: Wave Packets
Evolution of Wave Packets
We have seen, in Eq. (86), how to write the wavefunction of
a particle which is initially localized in 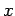 -space.
But,
how does this wavefunction evolve in time?
Well, according to Eq. (83), we have
-space.
But,
how does this wavefunction evolve in time?
Well, according to Eq. (83), we have
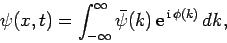 |
(97) |
where
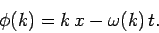 |
(98) |
The function 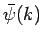 is obtained by Fourier transforming the
wavefunction at
is obtained by Fourier transforming the
wavefunction at  . See Eqs. (89) and (93). Now,
according to Eq. (95),
. See Eqs. (89) and (93). Now,
according to Eq. (95),
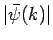 is strongly peaked around
is strongly peaked around  . Thus, it is a reasonable approximation
to Taylor expand
. Thus, it is a reasonable approximation
to Taylor expand  about
about  . Keeping terms up to
second-order in
. Keeping terms up to
second-order in  , we obtain
, we obtain
![\begin{displaymath}
\psi(x,t)\propto \int_{-\infty}^{\infty} \bar{\psi}(k)
\e...
...(k-k_0) + \frac{1}{2} \phi_0'' (k-k_0)^{ 2}\right\}\right],
\end{displaymath}](img360.png) |
(99) |
where
with
Substituting from Eq. (93), rearranging, and then changing the variable of integration to
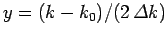 ,
we get
,
we get
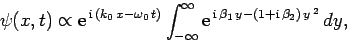 |
(106) |
where
Incidentally,
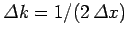 , where
, where 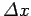 is the
initial width of the wave packet.
The above expression can be rearranged to give
is the
initial width of the wave packet.
The above expression can be rearranged to give
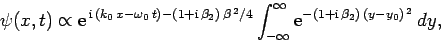 |
(109) |
where
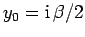 and
and
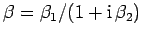 .
Again changing the variable of integration to
.
Again changing the variable of integration to
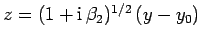 , we get
, we get
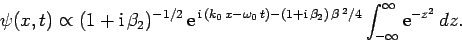 |
(110) |
The integral now just reduces to a number. Hence, we obtain
![\begin{displaymath}
\psi(x,t)\propto\frac{\exp\left[ {\rm i} (k_0 x-\omega_0\...
...[1+{\rm i} 2 \alpha ({\mit\Delta}k)^{ 2} t\right]^{1/2}},
\end{displaymath}](img385.png) |
(111) |
where
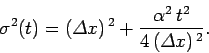 |
(112) |
Note that the above wavefunction is identical to our original wavefunction (86) at  . This, justifies the approximation which we made
earlier by Taylor expanding the phase factor
. This, justifies the approximation which we made
earlier by Taylor expanding the phase factor  about
about  .
.
According to Eq. (111), the probability density of our particle
as a function of time is written
![\begin{displaymath}
\vert\psi(x,t)\vert^{ 2} \propto \sigma^{-1}(t)\exp\left[-\frac{(x-x_0-v_g t)^{ 2}}{2 \sigma^{ 2}(t)}\right].
\end{displaymath}](img387.png) |
(113) |
Hence, the probability distribution is a Gaussian, of
characteristic width 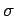 , which peaks at
, which peaks at 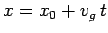 . Now, the
most likely position of our particle coincides with the peak of the
distribution function. Thus, the particle's most likely position is given by
. Now, the
most likely position of our particle coincides with the peak of the
distribution function. Thus, the particle's most likely position is given by
 |
(114) |
It can be seen that the particle effectively moves at the uniform velocity
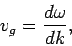 |
(115) |
which is known as the group velocity. In other words, a plane wave
travels at the phase velocity,  , whereas a wave packet travels
at the group velocity,
, whereas a wave packet travels
at the group velocity,
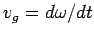 . Now, it follows from the dispersion
relation (79) for particle waves that
. Now, it follows from the dispersion
relation (79) for particle waves that
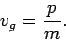 |
(116) |
However, it can be seen from Eq. (71) that this is identical
to the classical particle velocity. Hence, the dispersion relation (79) turns out to be consistent with classical physics, after all, as soon as we realize that
individual particles must be identified with wave packets rather than plane waves. In fact, a plane
wave is usually interpreted as a continuous stream of particles propagating in the same direction as the wave.
According to Eq. (112), the width of our wave packet
grows as time progresses. Indeed, it follows from Eqs. (79) and (105)
that the characteristic time for a wave packet of original width
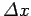 to double in spatial extent is
to double in spatial extent is
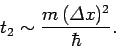 |
(117) |
For instance, if an electron is originally localized in a region of atomic scale (i.e.,
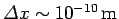 ) then the doubling time
is only about
) then the doubling time
is only about
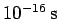 . Evidently, particle
wave packets (for freely moving particles) spread very rapidly.
. Evidently, particle
wave packets (for freely moving particles) spread very rapidly.
Note, from the previous analysis, that the rate of spreading of a wave packet is ultimately
governed by the second derivative of 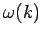 with respect to
with respect to 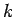 . See Eqs. (105) and (112). This is why a functional relationship between
. See Eqs. (105) and (112). This is why a functional relationship between 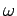 and
and 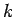 is generally known as a dispersion relation: i.e., because it
governs how wave packets disperse as time progresses.
However, for the special case where
is generally known as a dispersion relation: i.e., because it
governs how wave packets disperse as time progresses.
However, for the special case where 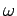 is a linear function
of
is a linear function
of 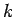 , the second derivative of
, the second derivative of 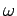 with respect to
with respect to 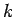 is zero,
and, hence, there is no dispersion of wave packets: i.e., wave packets
propagate without changing shape. Now, the dispersion relation
(50) for light waves is linear in
is zero,
and, hence, there is no dispersion of wave packets: i.e., wave packets
propagate without changing shape. Now, the dispersion relation
(50) for light waves is linear in 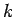 . It follows that light pulses
propagate through a vacuum without spreading. Another property
of linear dispersion relations is that the phase velocity,
. It follows that light pulses
propagate through a vacuum without spreading. Another property
of linear dispersion relations is that the phase velocity,  , and
the group velocity,
, and
the group velocity,
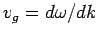 , are identical. Thus, both plane light waves
and light pulses propagate through a vacuum at the characteristic
speed
, are identical. Thus, both plane light waves
and light pulses propagate through a vacuum at the characteristic
speed
 . Of course, the dispersion relation (79) for particle waves is not linear in
. Of course, the dispersion relation (79) for particle waves is not linear in 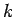 . Hence, particle
plane waves and particle wave packets propagate at different velocities,
and particle wave packets also gradually disperse as time progresses.
. Hence, particle
plane waves and particle wave packets propagate at different velocities,
and particle wave packets also gradually disperse as time progresses.



Next: Heisenberg's Uncertainty Principle
Up: Wave-Particle Duality
Previous: Wave Packets
Richard Fitzpatrick
2010-07-20
![\begin{displaymath}
\vert\psi(x,t)\vert^{ 2} \propto \sigma^{-1}(t)\exp\left[-\frac{(x-x_0-v_g t)^{ 2}}{2 \sigma^{ 2}(t)}\right].
\end{displaymath}](img387.png)
![]() to double in spatial extent is
to double in spatial extent is
![]() with respect to
with respect to ![]() . See Eqs. (105) and (112). This is why a functional relationship between
. See Eqs. (105) and (112). This is why a functional relationship between ![]() and
and ![]() is generally known as a dispersion relation: i.e., because it
governs how wave packets disperse as time progresses.
However, for the special case where
is generally known as a dispersion relation: i.e., because it
governs how wave packets disperse as time progresses.
However, for the special case where ![]() is a linear function
of
is a linear function
of ![]() , the second derivative of
, the second derivative of ![]() with respect to
with respect to ![]() is zero,
and, hence, there is no dispersion of wave packets: i.e., wave packets
propagate without changing shape. Now, the dispersion relation
(50) for light waves is linear in
is zero,
and, hence, there is no dispersion of wave packets: i.e., wave packets
propagate without changing shape. Now, the dispersion relation
(50) for light waves is linear in ![]() . It follows that light pulses
propagate through a vacuum without spreading. Another property
of linear dispersion relations is that the phase velocity,
. It follows that light pulses
propagate through a vacuum without spreading. Another property
of linear dispersion relations is that the phase velocity, ![]() , and
the group velocity,
, and
the group velocity,
![]() , are identical. Thus, both plane light waves
and light pulses propagate through a vacuum at the characteristic
speed
, are identical. Thus, both plane light waves
and light pulses propagate through a vacuum at the characteristic
speed
![]() . Of course, the dispersion relation (79) for particle waves is not linear in
. Of course, the dispersion relation (79) for particle waves is not linear in ![]() . Hence, particle
plane waves and particle wave packets propagate at different velocities,
and particle wave packets also gradually disperse as time progresses.
. Hence, particle
plane waves and particle wave packets propagate at different velocities,
and particle wave packets also gradually disperse as time progresses.