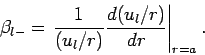Next: Hard Sphere Scattering
Up: Scattering Theory
Previous: Partial Waves
Let us now consider how the phase-shifts 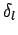 in Eq. (1306) can be
evaluated. Consider a spherically symmetric potential
in Eq. (1306) can be
evaluated. Consider a spherically symmetric potential 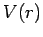 which
vanishes for
which
vanishes for 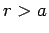 , where
, where 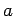 is termed the range of the potential.
In the region
is termed the range of the potential.
In the region 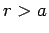 , the wavefunction
, the wavefunction 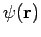 satisfies the free-space Schrödinger equation (1285). The
most general solution which is consistent with no incoming spherical-waves is
satisfies the free-space Schrödinger equation (1285). The
most general solution which is consistent with no incoming spherical-waves is
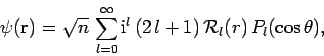 |
(1309) |
where
![\begin{displaymath}
{\cal R}_l(r) = \exp( {\rm i} \delta_l)
\left[\cos\delta_l j_l(k r) -\sin\delta_l y_l(k r)\right].
\end{displaymath}](img2944.png) |
(1310) |
Note that 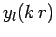 functions are allowed to appear in the above
expression, because its region of validity does not include the origin
(where
functions are allowed to appear in the above
expression, because its region of validity does not include the origin
(where 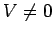 ). The logarithmic derivative of the
). The logarithmic derivative of the 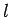 th
radial wavefunction,
th
radial wavefunction,
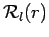 , just outside the range of the potential is given by
, just outside the range of the potential is given by
![\begin{displaymath}
\beta_{l+} = k a \left[\frac{ \cos\delta_l j_l'(k a) -
\s...
...}{\cos\delta_l
j_l(k a) - \sin\delta_l y_l(k a)}\right],
\end{displaymath}](img2947.png) |
(1311) |
where 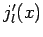 denotes
denotes 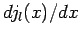 , etc. The above equation
can be inverted to give
, etc. The above equation
can be inverted to give
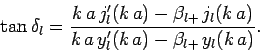 |
(1312) |
Thus, the problem of determining the phase-shift 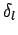 is equivalent
to that of obtaining
is equivalent
to that of obtaining 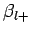 .
.
The most general solution to Schrödinger's equation inside
the range of the potential ( ) which does not depend on the
azimuthal angle
) which does not depend on the
azimuthal angle 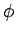 is
is
 |
(1313) |
where
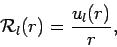 |
(1314) |
and
![\begin{displaymath}
\frac{d^2 u_l}{d r^2} +\left[k^2 -\frac{l (l+1)}{r^2} -\frac{2 m}{\hbar^2} V\right] u_l = 0.
\end{displaymath}](img2955.png) |
(1315) |
The boundary condition
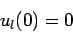 |
(1316) |
ensures that the radial wavefunction is well-behaved at the
origin.
We can launch a well-behaved solution of the above equation from
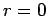 , integrate out to
, integrate out to  , and form the logarithmic derivative
, and form the logarithmic derivative
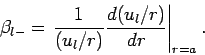 |
(1317) |
Since 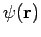 and its first derivatives are necessarily continuous for
physically acceptible wavefunctions, it follows that
and its first derivatives are necessarily continuous for
physically acceptible wavefunctions, it follows that
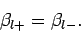 |
(1318) |
The phase-shift 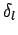 is then obtainable from Eq. (1312).
is then obtainable from Eq. (1312).



Next: Hard Sphere Scattering
Up: Scattering Theory
Previous: Partial Waves
Richard Fitzpatrick
2010-07-20
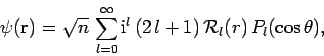
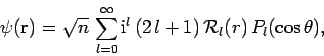
![\begin{displaymath}
\beta_{l+} = k a \left[\frac{ \cos\delta_l j_l'(k a) -
\s...
...}{\cos\delta_l
j_l(k a) - \sin\delta_l y_l(k a)}\right],
\end{displaymath}](img2947.png)
![]() ) which does not depend on the
azimuthal angle
) which does not depend on the
azimuthal angle ![]() is
is