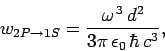Next: Intensity Rules
Up: Time-Dependent Perturbation Theory
Previous: Selection Rules
Let us calculate the rate of spontaneous emission between the
first excited state (i.e., 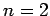 ) and the ground-state (i.e.,
) and the ground-state (i.e.,  ) of a hydrogen
atom. Now the ground-state is characterized by
) of a hydrogen
atom. Now the ground-state is characterized by 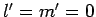 . Hence, in
order to satisfy the selection rules (1149) and (1150),
the excited state must have the quantum numbers
. Hence, in
order to satisfy the selection rules (1149) and (1150),
the excited state must have the quantum numbers 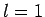 and
and 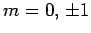 .
Thus, we are dealing with a spontaneous transition from a
.
Thus, we are dealing with a spontaneous transition from a 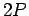 to a
to a  state. Note, incidentally, that a spontaneous transition from a
state. Note, incidentally, that a spontaneous transition from a  to a
to a  state
is forbidden by our selection rules.
state
is forbidden by our selection rules.
According to Sect. 9.4, the wavefunction of a hydrogen atom takes the form
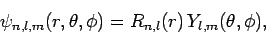 |
(1151) |
where the radial functions 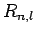 are given in Sect. 9.4,
and the spherical harmonics
are given in Sect. 9.4,
and the spherical harmonics 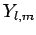 are given in Sect. 8.7.
Some straight-forward, but tedious, integration reveals that
are given in Sect. 8.7.
Some straight-forward, but tedious, integration reveals that
where 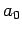 is the Bohr radius specified in Eq. (679).
All of the other possible
is the Bohr radius specified in Eq. (679).
All of the other possible
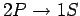 matrix elements are zero because of
the selection rules. If follows from Eq. (1144) that the modulus
squared of the dipole moment for the
matrix elements are zero because of
the selection rules. If follows from Eq. (1144) that the modulus
squared of the dipole moment for the
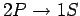 transition takes the same value
transition takes the same value
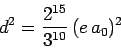 |
(1155) |
for 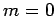 ,
, 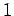 , or
, or 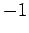 . Clearly, the transition rate is independent
of the quantum number
. Clearly, the transition rate is independent
of the quantum number  . It turns out that this is a general result.
. It turns out that this is a general result.
Now, the energy of the eigenstate of the hydrogen atom characterized
by the quantum numbers  ,
, 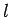 ,
,  is
is 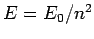 , where
the ground-state energy
, where
the ground-state energy 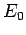 is specified in Eq. (678).
Hence, the energy of the photon emitted during a
is specified in Eq. (678).
Hence, the energy of the photon emitted during a
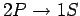 transition is
transition is
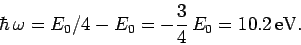 |
(1156) |
This corresponds to a wavelength of
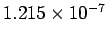 m.
m.
Finally, according to Eq. (1131), the
 transition rate
is written
transition rate
is written
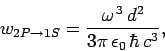 |
(1157) |
which reduces to
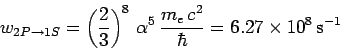 |
(1158) |
with the aid of Eqs. (1155) and (1156). Here,  is the fine-structure constant.
Hence, the mean
life-time of a hydrogen
is the fine-structure constant.
Hence, the mean
life-time of a hydrogen 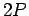 state is
state is
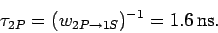 |
(1159) |
Incidentally, since the 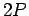 state only has a finite life-time, it follows from the
energy-time uncertainty relation that the energy of this
state is uncertain by an amount
state only has a finite life-time, it follows from the
energy-time uncertainty relation that the energy of this
state is uncertain by an amount
 |
(1160) |
This uncertainty gives rise to a finite width of the spectral
line associated with the
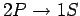 transition. This natural
line-width is of order
transition. This natural
line-width is of order
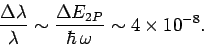 |
(1161) |



Next: Intensity Rules
Up: Time-Dependent Perturbation Theory
Previous: Selection Rules
Richard Fitzpatrick
2010-07-20
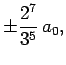
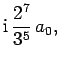
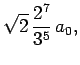
![]() ,
, ![]() ,
, ![]() is
is ![]() , where
the ground-state energy
, where
the ground-state energy ![]() is specified in Eq. (678).
Hence, the energy of the photon emitted during a
is specified in Eq. (678).
Hence, the energy of the photon emitted during a
![]() transition is
transition is
![]() transition rate
is written
transition rate
is written